
 如图,已知D、E分别为△ABC的边AB、AC上的点,F是线段DE上的任意一点,DE∥BC,且S△ABC=1,求证:△BDF和△CEF中至少有一个三角形的面积不大于
如图,已知D、E分别为△ABC的边AB、AC上的点,F是线段DE上的任意一点,DE∥BC,且S△ABC=1,求证:△BDF和△CEF中至少有一个三角形的面积不大于| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 2x |
| BC |
| h1 |
| h |
| 2xh |
| BC |
| 2xh |
| BC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |


科目:高中数学 来源: 题型:
| A、y=a(1+p%)x(0<x<m) |
| B、y=a(1-p%)x(0<x<m) |
| C、a(p%)x(0<x<m) |
| D、a-(p%)x(0<x<m) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:解答题
如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得PB=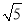 .点O为线段AD的中点,连接PO.
.点O为线段AD的中点,连接PO.
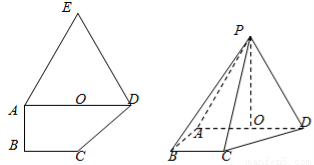
(1)求证:PO⊥平面ABCD;
(2)求二面角B-PC-D的大小的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
已知全集U=R,集合A={x|x2-2x<0},B={x|x-1≥0},那么集合A∩?UB=( )
A.{x|0<x<1} B.{x|x<0} C.{x|x>2} D.{x|1<x<2}
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
为了得到函数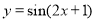 的图象,只需把函数
的图象,只需把函数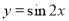 的图象上所有的点( )
的图象上所有的点( )
A.向右平行移动 个单位长度
个单位长度
B.向左平行移动 个单位长度
个单位长度
C.向左平行移动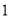 个单位长度
个单位长度
D.向右平行移动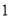 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com