
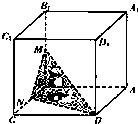
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是BB1,BC的中点,则图中阴影部分在平面ADD1A1上的投影的面积为
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是BB1,BC的中点,则图中阴影部分在平面ADD1A1上的投影的面积为 解:由题意知D点在投影面上,它的投影就是它本身,N在平面上的投影是AD棱的中点,M在平面上的投影是AA1的中点,
解:由题意知D点在投影面上,它的投影就是它本身,N在平面上的投影是AD棱的中点,M在平面上的投影是AA1的中点,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |


科目:高中数学 来源: 题型:
A、0,
| ||||||||
B、0,
| ||||||||
| C、0,π,2π,3π,4π | ||||||||
D、0,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知D、E分别为△ABC的边AB、AC上的点,F是线段DE上的任意一点,DE∥BC,且S△ABC=1,求证:△BDF和△CEF中至少有一个三角形的面积不大于
如图,已知D、E分别为△ABC的边AB、AC上的点,F是线段DE上的任意一点,DE∥BC,且S△ABC=1,求证:△BDF和△CEF中至少有一个三角形的面积不大于| 1 |
| 8 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=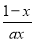 +lnx.
+lnx.
(1)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(2)设数列{bn}的前n项和为Sn,其中bn=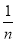 ,求证:当n≥2时,1+lnn>Sn.
,求证:当n≥2时,1+lnn>Sn.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:填空题
△ABC中,角A,B,C的对边分别为a,b,c,已知b=8,c=6,A=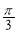 ,∠BAC的角平分线交边BC于点D,则|AD|=___________.
,∠BAC的角平分线交边BC于点D,则|AD|=___________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:解答题
设关于x的一元二次方程x2+2ax+b2=0
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个实数,b是从区间[0,2]任取的一个实数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:解答题
已知三棱柱ABC﹣A1B1C1的三视图及直观图如图所示,根据图中所给数据,解答下列问题:
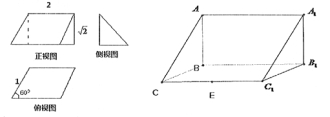
(1)求证:C1B⊥平面ABC;
(2)试在棱CC1(不包含端点C、C1)上确定一点E的位置,使得EA⊥EB1;
(3)求三棱柱ABC﹣A1B1C1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com