
已知三棱柱ABC﹣A1B1C1的三视图及直观图如图所示,根据图中所给数据,解答下列问题:
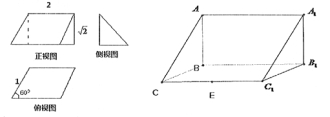
(1)求证:C1B⊥平面ABC;
(2)试在棱CC1(不包含端点C、C1)上确定一点E的位置,使得EA⊥EB1;
(3)求三棱柱ABC﹣A1B1C1的体积.
(1)见解析;(2)E为CC1中点;(3)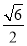 .
.
【解析】试题分析:(1)根据线面垂直的判定定理即可证明C1B⊥平面ABC;(2)根据线面垂直的性质,结合直角三角形的边长关系即可确定E的位置;(3)根据三棱柱ABC-A1B1C1的体积公式即可得到结论.
试题解析:(1)由三视图可知,AB⊥侧面BB1C1C,所以AB⊥BC1,
又BC=1,CC1=BB1=2,∠BCC1=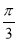
在△BCC1中,由余弦定理得BC1= ,故有BC2+BC12=CC12,
,故有BC2+BC12=CC12,
所以C1BBC
而BC∩AB=B,且AB,BC 平面ABC
平面ABC
所以C1B⊥平面ABC.
(2)由EA⊥EB1,AB⊥EB1,AB∩AE=A,AB,AE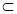 平面ABE
平面ABE
从而B1E⊥平面ABE
且BE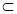 平面ABE,故BE⊥EB1,
平面ABE,故BE⊥EB1,
不妨设CE=x,则C1E=2-x
则BE2=1+x2-x
又因为∠B1C1C=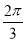 ,
,
则B1E2=x2-5x+7
在Rt△BEB1中,有(x2-5x+7)+(1+x2-x)=4
解得x=1或x=2(舍去)
故E为CC1的中点时,EA⊥EB1.
(3)由已知可得S△ABC=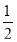 AB·BC=
AB·BC=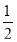 ×1×
×1× =
=
又由(1)知C1B⊥平面ABC,且C1B=
所以三棱柱ABC-A1B1C1的体积V=S△ABC·C1B=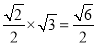
(或利用V=3VA-CBC1计算体积也可)
考点:空间线面关系,棱柱的体积


科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:选择题
设f(x)=4sinxsin +cos2x,|f(x)-m|<3对?x∈R恒成立,则实数m的范围是( )
+cos2x,|f(x)-m|<3对?x∈R恒成立,则实数m的范围是( )
A.(0,2] B.[0,2] C.[0,2) D.(0,2)
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)= (|x-a2|+|x-2a2|-3a2).若?x∈R,f(x-1)≤f(x),则实数a的取值范围为( )
(|x-a2|+|x-2a2|-3a2).若?x∈R,f(x-1)≤f(x),则实数a的取值范围为( )
A.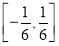 B.
B. C.
C.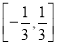 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
为了得到函数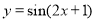 的图象,只需把函数
的图象,只需把函数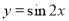 的图象上所有的点( )
的图象上所有的点( )
A.向右平行移动 个单位长度
个单位长度
B.向左平行移动 个单位长度
个单位长度
C.向左平行移动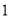 个单位长度
个单位长度
D.向右平行移动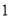 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:填空题
已知圆x2+y2+mx-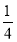 =0与抛物线y=
=0与抛物线y=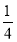 x2的准线相切,则m= _________ .
x2的准线相切,则m= _________ .
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
已知数列{an},若点{n,an}(n∈N*)在直线y+2=k(x﹣5)上,则数列{an}的前9项和S9=( )
A.18 B.﹣45 C.22 D.﹣18
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:选择题
对于三次函数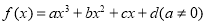 ,给出定义:设
,给出定义:设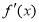 是函数
是函数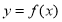 的导数,
的导数,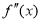 是
是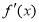 的导数,若方程
的导数,若方程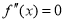 有实数解
有实数解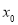 ,则称点
,则称点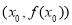 为函数
为函数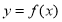 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数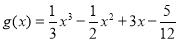 ,则
,则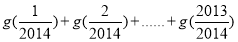 =( )
=( )
A. 2011 B. 2012 C. 2013 D. 2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com