
甲乙两人进行乒乓球比赛,各局相互独立,约定每局胜者得1分,负者得0分,如果两人比赛五局,乙得1分与得2分的概率恰好相等.
求乙在每局中获胜的概率为多少?
假设比赛进行到有一人比对方多2分或打满6局时停止,用 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.
【解析】(1) ;(2)
;(2)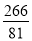 .
.
试题分析:(1)设每次比赛乙获胜的概率为 ,则两人比赛五局,乙得一分的概率为
,则两人比赛五局,乙得一分的概率为 ,乙得一分的概率为
,乙得一分的概率为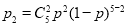 ,因为
,因为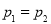 ,所以
,所以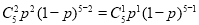 ,即可求得
,即可求得 ;
;
(2)由题意比赛进行到有一人比对方多2分或打满6局时停止,所以随机变量ξ的所有可能的取值为2,4,6,利用随机变量的定义及独立事件同时发生的概率公式求出每一个随机变量取值时对应的随机事件的概率,在有离散型随机的期望公式求出期望.
(1)设每次比赛乙获胜的概率为 ,则比赛5次乙恰好有
,则比赛5次乙恰好有 次获胜的概率为
次获胜的概率为 ,
,
由题设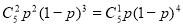 ,且
,且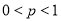 , 化简得
, 化简得 ,
,
所以,乙获胜的概率为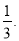
甲获胜的概率为
依题意知,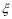 的所有可能值为2,4,6.
的所有可能值为2,4,6.
设每两局比赛为一轮,则该轮结束时比赛停止的概率为  .
.
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响.从而有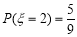 ,
,
 ,
, ,
,
故 .
.
考点:概率的应用;离散型随机变量的期望.


科目:高中数学 来源:2013-2014学年山东省德州市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
若函数 满足
满足 ,当x∈[0,1]时,
,当x∈[0,1]时, ,若在区间(-1,1]上, 方程
,若在区间(-1,1]上, 方程 有两个实数解,则实数m的取值范围是
有两个实数解,则实数m的取值范围是
A.0<m≤ B.0<m<
B.0<m<
C. <m≤l D.
<m≤l D. <m<1
<m<1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,输出的S值为( )
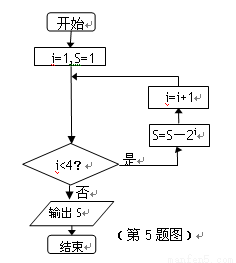
A. B.
B. C.
C. D.
D.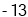
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
偶函数 满足
满足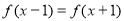 ,且在
,且在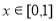 时,
时,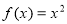 ,则关于
,则关于 的方程
的方程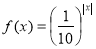 在
在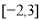 上的根的个数是 ( )
上的根的个数是 ( )
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考理科数学试卷(解析版) 题型:选择题
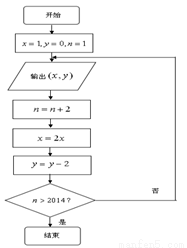
某程序框图如图所示,当输出 值为
值为 时,则输出
时,则输出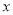 的值为( )
的值为( )
A.64 B.32 C.16 D.8
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:选择题
已知函数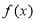 是定义在
是定义在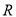 上的奇函数,对任意
上的奇函数,对任意 ,都有
,都有
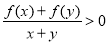 ,若
,若 ,则( )
,则( )
A. B.
B.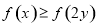
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com