
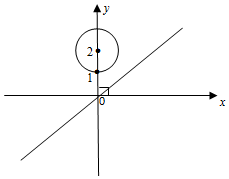
 已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线上,过点P作圆M的切线PA,PB,切点为A,B.
已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线上,过点P作圆M的切线PA,PB,切点为A,B.分析 (1)当切线斜率不存在时,切线方程为x=1,当切线斜率存在时,设直线方程为$y=k(x-1)+\frac{1}{2}$,由直线和圆相切,求出$k=-\frac{5}{12}$,由此能求出切线PA,PB方程.
(2)${S_{四边形PAMB}}=2×\frac{1}{2}×PA×MA=PA=\sqrt{P{M^2}-1}$,当PM最小时,四边形面积最小.由此能求出四边形PAMB面积的最小值.
(3)设点P(${x}_{0},\frac{1}{2}{x}_{0}$),M(0,2),过P,A,M三点的圆即以PM为直径的圆,由此能求出定点坐标.
解答 解:(1)当切线斜率不存在时,切线方程为x=1…(2分)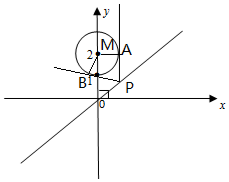
当切线斜率存在时,设直线方程为$y=k(x-1)+\frac{1}{2}$,
因为直线和圆相切,所以$d=\frac{{|{k+\frac{3}{2}}|}}{{\sqrt{{k^2}+1}}}=1$,解得$k=-\frac{5}{12}$,
此时直线方程为y=-$\frac{5}{12}$(x-1)+$\frac{1}{2}$,即5x+12y-11=0,
所以切线PA,PB方程x=1,5x+12y-11=0.…(4分)
(2)${S_{四边形PAMB}}=2×\frac{1}{2}×PA×MA=PA=\sqrt{P{M^2}-1}$…(6分)
故当PM最小时,四边形面积最小.而$PM≥\frac{{|{0-4}|}}{{\sqrt{5}}}=\frac{4}{{\sqrt{5}}}$
所以四边形PAMB面积的最小值${S_{min}}=\frac{{\sqrt{55}}}{5}$…(10分)
证明:(3)设点P(${x}_{0},\frac{1}{2}{x}_{0}$),M(0,2),
过P,A,M三点的圆即以PM为直径的圆
即($\frac{{x}_{0}}{2}$)2+($\frac{\frac{1}{2}{x}_{0}+2}{2}$)2=($\frac{\sqrt{{{x}_{0}}^{2}+(\frac{1}{2}{x}_{0}-2)^{2}}}{2}$)2,…(12分)
所以${x^2}-{x_0}x+{y^2}-(\frac{1}{2}{x_0}+2)y+{x_0}=0$,
从而$\left\{\begin{array}{l}{x^2}+{y^2}-2y=0\\-x-\frac{1}{2}y+1=0\end{array}\right.$,
解得定点坐标为(0,2)或($\frac{4}{5}$,$\frac{2}{5}$).…(16分)
点评 本题考查圆的切线方程、直线方程、四边形面积的求法,涉及到圆、直线方程、直线与圆相切等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
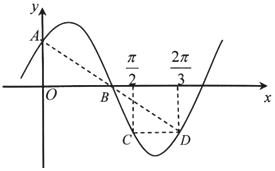 如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.
如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3]∪[4,+∞) | B. | [-3,4] | C. | (-∞,-2]∪[5,+∞) | D. | [-2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | $\frac{14}{3}$ | C. | $6+3\sqrt{5}$ | D. | $11+3\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
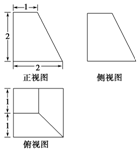
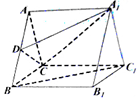 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com