
分析 (1)由a1,2a2,4a3成等差数列,可得2×2a2=a1+4a3,代入解出即可得出.
(2)由a2n-1=$(\frac{1}{2})^{2n-1}$,利用等比数列的前n项和公式即可得出.
解答 (1)解:∵a1,2a2,4a3成等差数列,∴2×2a2=a1+4a3,4×q=1+4q2,解得q=$\frac{1}{2}$.
∴an=$(\frac{1}{2})^{n}$.
(2)证明:a2n-1=$(\frac{1}{2})^{2n-1}$.
∴a1+a3+a5+…+a2n-1=$\frac{1}{2}$×$\frac{1-\frac{1}{{4}^{n}}}{1-\frac{1}{4}}$=$\frac{2}{3}$$(1-\frac{1}{{4}^{n}})$<$\frac{2}{3}$.
∴a1+a3+a5+…+a2n-1<$\frac{2}{3}$.
点评 本题考查了等差数列与等比数列的通项公式前n项和公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
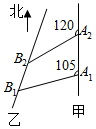 如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?
如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4029}{4031}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | $-\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | $-\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆O与离心率为$\frac{\sqrt{3}}{2}$的椭圆T:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个切点为M(2,0),O为坐标原点.
如图,圆O与离心率为$\frac{\sqrt{3}}{2}$的椭圆T:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个切点为M(2,0),O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com