
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,点M在线段PC上,且PM=2MC,N为AD的中点.分析 (1)由题意证明△PNA≌△BNA,得到BN⊥AD,再由线面垂直的判定证得AD⊥平面PNB,最后由面面垂直的判定得答案;
(2)由面面垂直的性质得到PN⊥平面ABCD,进一步得到PN⊥BN,再由等积法把三棱锥P-NBM的体积转化为棱锥C-PNB的体积求解.
解答 (1)证明:∵PA=PD,N为AD的中点,∴PN⊥AD,
∵底面ABCD为菱形,∠BAD=60°,∴PA=AB,AN=AN,∠PAN=∠BAN,
∴△PNA≌△BNA,则BN⊥AD,
∵PN∩BN=N,∴AD⊥平面PNB,
又AD?平面PAD,∴平面PAD⊥平面PNB;
(2)解:∵PA=PD=AD=2,∴PN=NB=$\sqrt{3}$,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PN⊥AD,
∴PN⊥平面ABCD,∴PN⊥BN,
∴S△PNB=$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{3}$=$\frac{3}{2}$,
∵AD⊥平面PNB,AD∥BC,∴BC⊥平面PNB,
∵PM=2MC,∴VP-NBM=VM-PNB=$\frac{2}{3}$VC-PNB=$\frac{2}{3}$×$\frac{1}{3}$×$\frac{3}{2}$×2=$\frac{2}{3}$.
点评 本题考查平面与平面垂直的判定,考查了棱锥、棱柱、棱台体积的求法,考查了空间想象能力和思维能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:填空题
已知矩形 的顶点都在半径为
的顶点都在半径为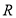 的球
的球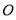 的球面上,且
的球面上,且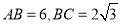 ,棱锥
,棱锥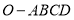 的体积为
的体积为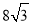 ,则
,则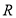 = ________.
= ________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
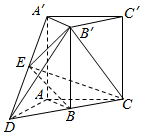 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2.
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
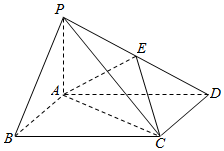 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com