
分析 直接利用等差数列的通项公式先确定数列的首相,进一步利用前n项和公式求出${S}_{n}=2{n}^{2}+\frac{9}{2}n$,最后利用系数对应相等求出结果.
解答 解:数列{an}中,an=4n+$\frac{5}{2}$,
所以:${a}_{1}=\frac{13}{2}$,
则:Sn=a1+a2+…+an
=$\frac{n(\frac{13}{2}+4n+\frac{5}{2})}{2}$
=$\frac{4{n}^{2}+9n}{2}=2{n}^{2}+\frac{9}{2}n$
=an2+bn,
所以:a=2,b=$\frac{9}{2}$,
则:ab=9
故答案为:9
点评 本题考查的知识要点:等差数列前n项和公式的应用,主要考查学生的应用能力.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
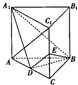 已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.
已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | a<c<b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量V(件) | 90 | 84 | 83 | 80 | 75 | 68 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一个几何体的三视图如图所示,(其中的长度单位为cm),其中俯视图是一个腰长为2cm的等腰直角三角形,则这几何体外接球的表面积为12πcm2.
一个几何体的三视图如图所示,(其中的长度单位为cm),其中俯视图是一个腰长为2cm的等腰直角三角形,则这几何体外接球的表面积为12πcm2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,若∠OFB=$\frac{π}{6}$,$\overrightarrow{OF}•\overrightarrow{FB}$=-6,则以OA为长半轴,OB为短半轴,F为左焦点的椭圆的标准方程为$\frac{{x}^{2}}{8}$$+\frac{{y}^{2}}{2}$=1.
如图,若∠OFB=$\frac{π}{6}$,$\overrightarrow{OF}•\overrightarrow{FB}$=-6,则以OA为长半轴,OB为短半轴,F为左焦点的椭圆的标准方程为$\frac{{x}^{2}}{8}$$+\frac{{y}^{2}}{2}$=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com