
| A. | [0,4] | B. | [4,+∞) | C. | ($\frac{1}{4}$,+∞) | D. | (-∞,$\frac{1}{4}$] |
分析 首先判断出x=0是方程的一个实数解,所以$\frac{|x|}{x+4}=k{x^2}$有三个不同的非零实数解;然后判断出g(x)=$\frac{1}{k}$=$\left\{\begin{array}{l}x(x+4),x>0\\-x(x+4),x<0\end{array}\right.$,根据其函数图象,要使$\frac{|x|}{x+4}=k{x^2}$有三个不同的非零实数解,求出k的取值范围即可.
解答 解:∵$\frac{|x|}{x+4}=k{x}^{2}$,
∴x=0是方程的一个实数解,
又∵关于x的方程$\frac{|x|}{x+4}=k{x^2}$有4个不同的实根,
∴$\frac{|x|}{x+4}=k{x^2}$有三个不同的非零实数解.
(1)当x>0时,
由$\frac{x}{x+4}=k{x}^{2}$,
可得$\frac{1}{k}$=x(x+4);
(2)当x<0时,
由-$\frac{x}{x+4}=k{x}^{2}$,
可得$\frac{1}{k}$=-x(x+4);
∴g(x)=$\frac{1}{k}$=$\left\{\begin{array}{l}x(x+4),x>0\\-x(x+4),x<0\end{array}\right.$,如图1,
要使$\frac{|x|}{x+4}=k{x^2}$有三个不同的非零实数解,
则0<$\frac{1}{k}$<4,
∴k>$\frac{1}{4}$.
故选:C.
点评 此题主要考查了分式方程的解,要熟练掌握,注意数形结合方法的应用,解答此题的关键是判断出:g(x)=$\frac{1}{k}$=$\left\{\begin{array}{l}x(x+4),x>0\\-x(x+4),x<0\end{array}\right.$,考查数形结合的应用.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
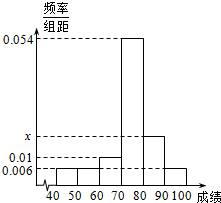 某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | $({-1,\frac{{1-\sqrt{5}}}{2}})$ | C. | $({\frac{{1-\sqrt{5}}}{2},0})$ | D. | $({0,\frac{{1+\sqrt{5}}}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com