
分析 本题考查的知识点是设计程序框图解决实际问题,我们根据题目已知中分段函数的解析式y=$\left\{\begin{array}{l}{0.1x}&{x≤30}\\{3+0.2(x-30)}&{x>30}\end{array}\right.$,然后根据分类标准,设置两个判断框的并设置出判断框中的条件,再由函数各段的解析式,确定判断框的“是”与“否”分支对应的操作,由此即可画出流程图,再编写满足题意的程序.
解答 解:程序为:
INPUT x
IF x<=30 THEN
y=0.1*x
ELSE
y=3+0.2*(x-30)
END IF
PRINT y
END
点评 本题考查了设计程序框图解决实际问题,主要考查编写程序解决分段函数问题,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 38 | B. | 20 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
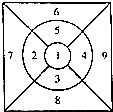 如图,图案共分9个区域,有6种不同颜色的涂料可供涂色,每个区域只能涂一种颜色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相邻区域的颜色不相同,则涂色方法有( )
如图,图案共分9个区域,有6种不同颜色的涂料可供涂色,每个区域只能涂一种颜色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相邻区域的颜色不相同,则涂色方法有( )| A. | 360种 | B. | 720种 | C. | 780种 | D. | 840种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{4}{3}$ | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=x0,g(x)=13x | ||
| C. | f(x)=3x,g(x)=($\frac{1}{3}$)-x | D. | f(x)=x-1,g(x)=$\frac{{x}^{2}-1}{x+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com