
 如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论. 分析 推导出AB与l一定相交.设AB∩l=P,则P∈AB,P∈l,则点P是平面ABC与β的一个公共点,从而直线PC就是平面ABC与β的交线,由此能证明平面ABC与β的交线与l相交.
解答 解:平面ABC与平面β的交线与l相交.
证明∵AB与l不平行,且AB?α,l?α,
∴AB与l一定相交.设AB∩l=P,则P∈AB,P∈l.
又∵AB?平面ABC,l?β,∴P∈平面ABC,P∈β.
∴点P是平面ABC与β的一个公共点.
而点C也是平面ABC与β的一个公共点,且P,C是不同的两点,
∴直线PC就是平面ABC与β的交线,
即平面ABC∩β=PC,而PC∩l=P.
∴平面ABC与β的交线与l相交.
点评 本题考查两平面的交线与已知直线的位置关系的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1.4,2) | B. | (1,1.4) | C. | (1,1.5) | D. | (1.5,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
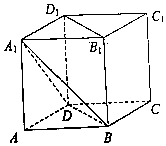 如图,在正方体ABCD-A1B1C1D1中,AB=2,过直线B1D1的平面α⊥平面A1BD,则平面α截该正方体所得截面的面积为$\sqrt{6}$ .
如图,在正方体ABCD-A1B1C1D1中,AB=2,过直线B1D1的平面α⊥平面A1BD,则平面α截该正方体所得截面的面积为$\sqrt{6}$ .查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com