
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
分析 这是一个几何概型中的面积类型,则分别求得试验的全部结果的构成的区域Ω={(x,y)|-1≤x≤1,-1≤y≤1}的面积和两个数的平方和小于1所构成的区域A={(x,y)|x2+y2<1,-1≤x≤1,-1≤y≤1}的面积,然后再求比值即为所求的概率.
解答 解:设两个数的平方和小于1的概率为P
从[-1,1]内任意取两个实数为:x,y
试验的全部结果的构成的区域为Ω={(x,y)|-1≤x≤1,-1≤y≤1}
其面积为:SΩ=4,
两个数的平方和小于1所构成的区域为:A={(x,y)|x2+y2<1,-1≤x≤1,-1≤y≤1},其面积为:SA=π
∴P(A)=$\frac{{S}_{A}}{{S}_{Ω}}$=$\frac{π}{4}$,
故选:D
点评 本题主要考查几何概型中的面积类型及其应用,基本方法是:分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积,两者求比值,即为概率.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,4) | C. | (3,4) | D. | (4,8] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=x0,g(x)=13x | ||
| C. | f(x)=3x,g(x)=($\frac{1}{3}$)-x | D. | f(x)=x-1,g(x)=$\frac{{x}^{2}-1}{x+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
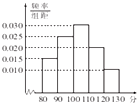 某班k名学生在一次考试中数学成绩绘制的频率分布直方图如图,若在这k名学生中,数学成绩不低于90分的人数为34,则k=( )
某班k名学生在一次考试中数学成绩绘制的频率分布直方图如图,若在这k名学生中,数学成绩不低于90分的人数为34,则k=( )| A. | 40 | B. | 46 | C. | 48 | D. | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com