
 经过点
经过点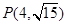 ,且双曲线
,且双曲线 的渐近线与圆
的渐近线与圆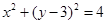 相切.
相切. 的方程;
的方程;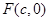 是双曲线
是双曲线 的右焦点,
的右焦点,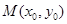 是双曲线
是双曲线 的右支上的任意一点,试判断以
的右支上的任意一点,试判断以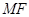 为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.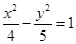 ;(2)外切.
;(2)外切.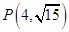 在双曲线
在双曲线 上”以及“双曲线
上”以及“双曲线 的渐近线与圆
的渐近线与圆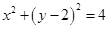 ”这两个条件列两个方程,求解
”这两个条件列两个方程,求解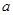 与
与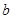 ,进而确定双曲线
,进而确定双曲线 的方程;(2)根据圆与圆的位置关系的判断方法,考查两圆连心线的长度与两圆半径之间的相互关系,同时注意将点
的方程;(2)根据圆与圆的位置关系的判断方法,考查两圆连心线的长度与两圆半径之间的相互关系,同时注意将点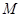 与左焦点
与左焦点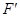 连接起来,注意到两圆圆心分别为
连接起来,注意到两圆圆心分别为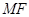 与
与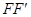 的中点,利用中位线以及双曲线的定义确定两圆半径与连心线长度之间的关系,进而确定两圆的位置关系.
的中点,利用中位线以及双曲线的定义确定两圆半径与连心线长度之间的关系,进而确定两圆的位置关系.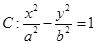 经过点
经过点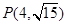 ,所以
,所以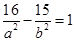 ①.
①. 的的渐近线
的的渐近线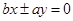 与圆
与圆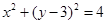 相切,
相切,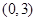 到直线
到直线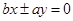 的距离等于2,
的距离等于2,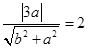 ,整理得
,整理得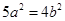 ②.
②.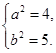 所以双曲线
所以双曲线 的方程为
的方程为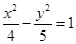 .
.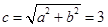 ,所以双曲线
,所以双曲线 的右焦点为
的右焦点为 .
. 的左焦点为
的左焦点为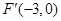 ,因为点
,因为点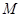 在双曲线
在双曲线 的右支上,
的右支上,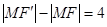 ,即
,即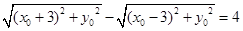 ,
, .
. 的实轴为直径的圆的圆心为
的实轴为直径的圆的圆心为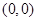 ,半径为
,半径为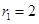 ;
;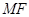 为直径的圆的圆心为
为直径的圆的圆心为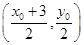 ,半径为
,半径为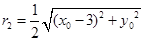 ,
,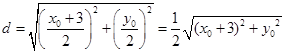 .
.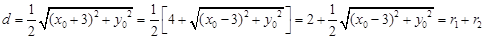 ,
,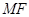 为直径的圆与以双曲线实轴为直径的圆外切.
为直径的圆与以双曲线实轴为直径的圆外切.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com