
分析 (1)利用向量的平方与其模长平方相等,转化为数量积的运算,然后开方求值;
(2)利用向量平行的性质得到$\overrightarrow c=λ\overrightarrow d$,借助于平面向量基本定理得到m的值.
解答 解:(1)$\overrightarrow a•\overrightarrow b=\frac{1}{2}$,
∴${|{\overrightarrow a+3\overrightarrow b}|^2}={|a|^2}+6\overrightarrow a•\overrightarrow b+9{|{\overrightarrow b}|^2}=13$,
∴$|{\overrightarrow a+3\overrightarrow b}|=\sqrt{13}$…4分
(2)当$\overrightarrow c$∥$\overrightarrow d$,则存在实数λ使$\overrightarrow c=λ\overrightarrow d$,所以$3\overrightarrow a+2\overrightarrow b=λ(m\overrightarrow a-4\overrightarrow b)$
∵$\overrightarrow a,\overrightarrow b$不共线
∴$\left\{\begin{array}{l}3=λm\\ 2=-4λ\end{array}\right.$
∴m=-6…(8分)
点评 本题考查了平面向量的模长计算以及平行的性质、平面向量基本定理;属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
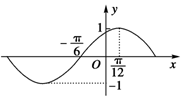
| A. | $y=sin(x+\frac{π}{6})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(2x+\frac{π}{6})$ | D. | $y=sin(2x+\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${({\sqrt{2}+\sqrt{7}})^2}<{({\sqrt{3}+\sqrt{6}})^2}$ | B. | ${({\sqrt{2}-\sqrt{6}})^2}<{({\sqrt{3}-\sqrt{7}})^2}$ | C. | ${({\sqrt{2}-\sqrt{3}})^2}<{({\sqrt{6}-\sqrt{7}})^2}$ | D. | ${({\sqrt{2}-\sqrt{3}-\sqrt{6}})^2}<{({-\sqrt{7}})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com