
已知函数 .
.
(1)求 的定义域;
的定义域;
(2)讨论 的奇偶性;
的奇偶性;
(3)讨论 的单调性.
的单调性.
(1)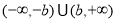 ;(2)奇函数;(3)当
;(2)奇函数;(3)当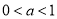 时,
时,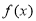 在
在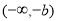 和
和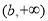 上是增函数;当
上是增函数;当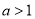 时,
时,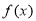 在
在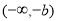 和
和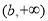 上是减函数.
上是减函数.
【解析】
试题分析:解题思路:(1)利用对数式的真数大于0解不等式即可;(2)验证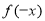 与
与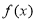 的关系;(3)利用复合函数的单调性证明判定.规律总结:1.函数定义域的求法:①分式中分母不为0;②偶次方根被开方数非负;③
的关系;(3)利用复合函数的单调性证明判定.规律总结:1.函数定义域的求法:①分式中分母不为0;②偶次方根被开方数非负;③ 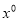 中
中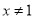 ;④对数式中底数为大于0且不等于1的实数,真数大于0;⑤正切函数的定义域为
;④对数式中底数为大于0且不等于1的实数,真数大于0;⑤正切函数的定义域为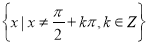 ;
;
2.复合函数单调性的判定原则“同增异减”.
试题解析:(1)令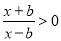 ,解得
,解得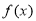 的定义域为
的定义域为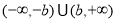 .
.
(2)因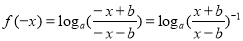
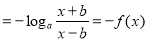 ,
,
故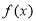 是奇函数.
是奇函数.
(3)令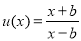 ,则函数
,则函数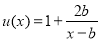 在
在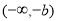 和
和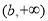 上是减函数,所以当
上是减函数,所以当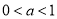 时,
时,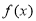 在
在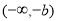 和
和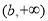 上是增函数;当
上是增函数;当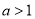 时,
时,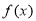 在
在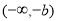 和
和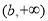 上是减函数.
上是减函数.
考点:1.函数的定义域;2.函数的奇偶性;3.复合函数的单调性.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一文科数学试卷(解析版) 题型:选择题
在等差数列 中,
中, =
= ,则数列
,则数列 的前11项和
的前11项和 =( ).
=( ).
A.24 B.48 C.66 D.132
查看答案和解析>>
科目:高中数学 来源:2015届河北唐山一中高二下学期期末考试文科数学试卷(解析版) 题型:选择题
如图给出的是计算 的值的一个程序框图,其中判断框内应填入
的值的一个程序框图,其中判断框内应填入
的条件是( )
A. B.
B.
C. D.
D.

查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末理数学卷(解析版) 题型:选择题
已知函数 =
=  ,
, =
= ,若至少存在一个
,若至少存在一个 ∈[1,e],使
∈[1,e],使 成立,则实数a的范围为( ).
成立,则实数a的范围为( ).
A.[1,+∞) B.(0,+∞) C.[0,+∞) D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末理数学卷(解析版) 题型:选择题
条件 ,条件
,条件 ,则p是q的( ).
,则p是q的( ).
A.充分不必要条件B.必要不充分条件  充要条件 D.既不充分又不必要条件
充要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末文数学卷(解析版) 题型:选择题
已知 在区间(0,+∞)上是减函数,那么
在区间(0,+∞)上是减函数,那么 与
与 的大小关系是( ).
的大小关系是( ).
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
| 轿车A | 轿车B | 轿车C |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com