
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
| 轿车A | 轿车B | 轿车C |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
(1) ;(2)
;(2)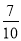 .
.
【解析】
试题分析:(1)根据分层抽样的相关理论,应该保证样本中三类轿车的比例与总体中三类轿车的比例保持一致,因此可设该厂本月生产轿车为n辆,列方程 ,
,
∴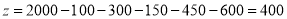 ;(2)由(1)中所求,以及分层抽样的相关理论,可得样本中的舒适型与标准型的轿车比例也为
;(2)由(1)中所求,以及分层抽样的相关理论,可得样本中的舒适型与标准型的轿车比例也为 ,所以可得样本中抽取了2辆舒适性轿车,3辆标准型轿车,所求概率为至少有一辆舒适型轿车,可以考虑其对立事件:没有一辆车是是舒适型轿车,即所有抽取的轿车都是标准型轿车,再由古典概型与对立事件概率的相关理论,可以求得至少有一辆舒适型轿车的概率为
,所以可得样本中抽取了2辆舒适性轿车,3辆标准型轿车,所求概率为至少有一辆舒适型轿车,可以考虑其对立事件:没有一辆车是是舒适型轿车,即所有抽取的轿车都是标准型轿车,再由古典概型与对立事件概率的相关理论,可以求得至少有一辆舒适型轿车的概率为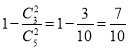 .
.
(1) 设该厂本月生产轿车为n辆,由题意得, 3分
3分
所以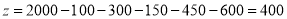 6分;
6分;
设所抽样本中有m辆舒适型轿车,因用分层抽样的方法在C类轿车中抽取一个容量为5的样本,
所以 ,解得
,解得 ,也即抽取了2辆舒适型轿车,3辆标准型轿车 8分
,也即抽取了2辆舒适型轿车,3辆标准型轿车 8分
所以从中任取2辆,至少有1辆舒适型轿车的概率为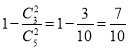 12分.
12分.
考点:1.分层抽样;2.古典概型与对立事件.


科目:高中数学 来源:2015届江西省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数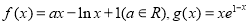 。
。
(1)求函数 在区间
在区间 上的值域;
上的值域;
(2)是否存在实数a,对任意给定的 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的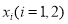 ,使得
,使得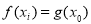 成立.若存在,求出a的取值范围;若不存在,请说明理由.
成立.若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
下表是甲、乙两个班级进行数学考试,按学生考试及格及不及格统计成绩后的2×2列联表:则 的值为( )
的值为( )
| 不及格 | 及格 | 合计 |
甲班 | 12 | 33 | 45 |
乙班 | 9 | 36 | 45 |
合计 | 21 | 69 | 90 |
A.0.559 B.0.456 C.0.443 D.0.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com