Question

11．在平面直角坐标系xOy中，已知P点到两定点D（-2，0），E（2，0）连线斜率之积为$-\frac{1}{2}$．
（1）求证：动点P恒在一个定椭圆C上运动；
（2）过$F（\sqrt{2}，0）$的直线交椭圆C于A，B两点，过O的直线交椭圆C于M，N两点，若直线AB与直线MN斜率之和为零，求证：直线AM与直线BN斜率之和为定值．

Answer 1

分析 （1）设P（x，y），由题意可得k_PD•k_PE=-$\frac{1}{2}$，运用直线的斜率公式，化简即可得到所求轨迹方程；
（2）设过F的直线为x=my+$\sqrt{2}$，代入椭圆方程x²+2y²=4，设A（x₁，y₁），B（x₂，y₂），运用韦达定理，点满足直线方程，再由过O的直线x=-my交椭圆C于M，N两点，求得M，N的坐标，运用直线的斜率公式，化简整理，即可得到直线AM与直线BN斜率之和为定值0．

解答 解：（1）设P（x，y），由题意可得k_PD•k_PE=-$\frac{1}{2}$，
即有$\frac{y}{x+2}$•$\frac{y}{x-2}$=-$\frac{1}{2}$，
化为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1；
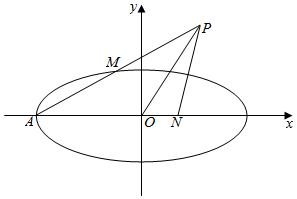
（2）设过F的直线为x=my+$\sqrt{2}$，
代入椭圆方程x²+2y²=4，
可得（2+m²）y²+2$\sqrt{2}$my-2=0，
设A（x₁，y₁），B（x₂，y₂），
即有y₁+y₂=-$\frac{2\sqrt{2}m}{2+{m}^{2}}$，y₁y₂=-$\frac{2}{2+{m}^{2}}$，
x₁=my₁+$\sqrt{2}$，x₂=my₂+$\sqrt{2}$，
由题意可得，过O的直线x=-my交椭圆C于M，N两点，
解得M（-$\frac{2m}{\sqrt{2+{m}^{2}}}$，$\frac{2}{\sqrt{2+{m}^{2}}}$），N（$\frac{2m}{\sqrt{2+{m}^{2}}}$，-$\frac{2}{\sqrt{2+{m}^{2}}}$），
可得k_AM+k_BN=$\frac{{y}_{1}-\frac{2}{\sqrt{2+{m}^{2}}}}{{x}_{1}+\frac{2m}{\sqrt{2+{m}^{2}}}}$+$\frac{{y}_{2}+\frac{2}{\sqrt{2+{m}^{2}}}}{{x}_{2}-\frac{2m}{\sqrt{2+{m}^{2}}}}$，
通分后的分子=x₂y₁-$\frac{2}{\sqrt{2+{m}^{2}}}$x₂-$\frac{2m}{\sqrt{2+{m}^{2}}}$y₁+x₁y₂+$\frac{2}{\sqrt{2+{m}^{2}}}$x₁+$\frac{2m}{\sqrt{2+{m}^{2}}}$y₂+$\frac{8m}{2+{m}^{2}}$
=2my₁y₂+$\sqrt{2}$（y₁+y₂）+$\frac{2}{\sqrt{2+{m}^{2}}}$（x₁-x₂）+$\frac{2m}{\sqrt{2+{m}^{2}}}$（y₂-y₁）+$\frac{8m}{2+{m}^{2}}$
=-$\frac{4m}{2+{m}^{2}}$-$\frac{4m}{2+{m}^{2}}$+$\frac{2m}{\sqrt{2+{m}^{2}}}$（y₁-y₂）+$\frac{2m}{\sqrt{2+{m}^{2}}}$（y₂-y₁）+$\frac{8m}{2+{m}^{2}}$=0．
即有直线AM与直线BN斜率之和为定值0．

点评 本题考查轨迹方程的求法，注意运用直线的斜率公式，考查直线的斜率之和为定值，注意联立直线方程和椭圆方程，运用韦达定理和斜率公式，化简整理，考查运算能力，属于中档题．