
| 空气质量指数 | (0,35] | [35,75] | (75,115] | (115,150] | (150,250] | >250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
| 乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
分析 (Ⅰ)以频率值作为概率值,利用等可能事件概率计算公式能求出甲区和乙区通过监测的概率$\frac{4}{5}$.
(Ⅱ)随机变量X的所有可能取值为90,45,30,-15,分别求出相应的概率,由此能求出随机变量X的分布列和EX.
解答 解:(Ⅰ)由题意得甲区通过监测的概率约为:$\frac{42+20+13}{100}=\frac{3}{4}$,
乙区通过监测的概率约为:$\frac{40+32+8}{100}$=$\frac{4}{5}$.
(Ⅱ)随机变量X的所有可能取值为90,45,30,-15,
P(X=90)=$\frac{4}{5}×\frac{3}{4}=\frac{3}{5}$,
P(X=45)=$\frac{4}{5}×\frac{1}{4}$=$\frac{1}{5}$,
P(X=30)=$\frac{1}{5}×\frac{3}{4}$=$\frac{3}{20}$,
P(X=-15)=$\frac{1}{5}×\frac{1}{4}$=$\frac{1}{20}$,
∴随机变量X的分布列为:
| X | 90 | 45 | 30 | -15 |
| P | $\frac{3}{50}$ | $\frac{1}{50}$ | $\frac{3}{20}$ | $\frac{1}{20}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
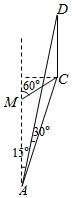 如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.
如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| a | b | c | d | |
| a | a13胜26负 | a20胜10负 | a21胜21负 | |
| b | b26胜13负 | b14胜28负 | b19胜19负 | |
| c | c10胜20负 | c28胜14负 | c18胜18负 | |
| d | d21胜21负 | d19胜19负 | d18胜18负 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 超速分组 | 频数 | 频率 | 频率 组距 |
| 1 | [0,20%] | 176 | 0.88 | z |
| 2 | [20%,40%] | 12 | 0.06 | 0.0030 |
| 3 | [40%,60%] | 6 | y | 0.0015 |
| 4 | [60%,80%] | 4 | 0.02 | 0.0010 |
| 5 | [80%,100%] | x | 0.01 | 0.0005 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com