
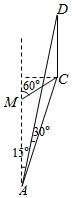
 如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.
如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m. 分析 在△ACM中由正弦定理解出AC,在Rt△ACD中,根据三角函数的定义得出CD.
解答 解:在△ACM中,∠MCA=60°-15°=45°,∠AMC=180°-60°=120°,
由正弦定理得$\frac{AM}{sin∠MCA}=\frac{AC}{sin∠AMC}$,即$\frac{1200}{\frac{\sqrt{2}}{2}}=\frac{AC}{\frac{\sqrt{3}}{2}}$,解得AC=600$\sqrt{6}$.
在△ACD中,∵tan∠DAC=$\frac{DC}{AC}$=$\frac{\sqrt{3}}{3}$,
∴DC=ACtan∠DAC=600$\sqrt{6}$×$\frac{\sqrt{3}}{3}$=600$\sqrt{2}$.
故答案为:600$\sqrt{2}$.
点评 本题考查了解三角形的应用,寻找合适的三角形是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | i | B. | {i} | C. | {0,i} | D. | {-i,0,i} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
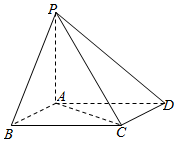 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )| A. | [$\frac{\sqrt{2}}{6}$,$\frac{1}{3}$) | B. | ($\frac{\sqrt{2}}{12}$,$\frac{1}{6}$] | C. | ($\frac{\sqrt{2}}{6}$,$\frac{1}{3}$] | D. | [$\frac{\sqrt{2}}{12}$,$\frac{1}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数 | (0,35] | [35,75] | (75,115] | (115,150] | (150,250] | >250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
| 乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [1,2] | C. | [1,+∞) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是真命题且q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
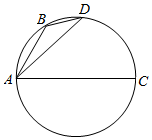 如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com