
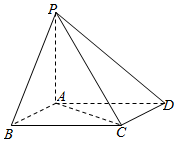
 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )| A. | [$\frac{\sqrt{2}}{6}$,$\frac{1}{3}$) | B. | ($\frac{\sqrt{2}}{12}$,$\frac{1}{6}$] | C. | ($\frac{\sqrt{2}}{6}$,$\frac{1}{3}$] | D. | [$\frac{\sqrt{2}}{12}$,$\frac{1}{6}$) |
分析 先根据条件得到四边形ABCD的面积S=sinθ,由余弦定理可求得AC=$\sqrt{2-2cosθ}$,即可得到PA,进而表示出四棱锥P-ABCD的体积,整理后再借助于三角函数的取值范围即可解题.
解答 解:S菱形ABCD=$2•\frac{1}{2}AB•BC•sinθ$=sinθ,
在△ABC中,由余弦定理得AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BCcosθ}$=$\sqrt{2-2cosθ}$.
∵PA•AC=1,∴PA=$\frac{1}{\sqrt{2-2cosθ}}$.
∴四棱锥P-ABCD的体积V=$\frac{1}{3}{S}_{菱形ABCD}•PA$=$\frac{\sqrt{2}}{6}×$$\sqrt{\frac{si{n}^{2}θ}{1-cosθ}}$=$\frac{\sqrt{2}}{6}×\sqrt{1+cosθ}$.
∵0<θ≤$\frac{π}{2}$,∴0≤cosθ<1.∴$\frac{\sqrt{2}}{6}$≤V<$\frac{1}{3}$.
故选:A.
点评 本题考查了余弦定理,三角函数的最值,棱锥的体积计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.
如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
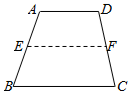 如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.
如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45°,点E,F分别是AC,AD的中点.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45°,点E,F分别是AC,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
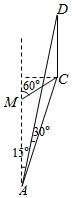 如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.
如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
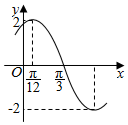 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )| A. | $[kπ-\frac{π}{3},kπ+\frac{π}{6}]$,k∈Z | B. | $[kπ+\frac{π}{6},kπ+\frac{2π}{3}]$,k∈Z | ||
| C. | $[kπ-\frac{π}{12},kπ+\frac{π}{12}]$,k∈Z | D. | $[kπ-\frac{7π}{12},kπ-\frac{π}{12}]$,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com