
【题目】如图,在三棱柱中![]() ,点P,G分别是AD,EF的中点,已知
,点P,G分别是AD,EF的中点,已知![]() 平面ABC,AD=EF=3,DE=DF=2.
平面ABC,AD=EF=3,DE=DF=2.
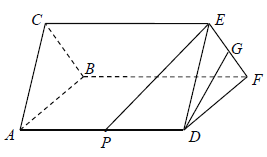
(Ⅰ)求证:DG⊥平面BCEF;
(Ⅱ)求PE与平面BCEF 所成角的正弦值.
【答案】( Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析: (Ⅰ)要证![]() 与平面
与平面![]() 垂直,就要证
垂直,就要证![]() 与平面
与平面![]() 内两条相交直线垂直,其中一条由等腰三角形的性质可得,即
内两条相交直线垂直,其中一条由等腰三角形的性质可得,即![]() ,再由已知
,再由已知![]() 平面
平面![]() ,即三棱柱侧棱与底面垂直,因此可得
,即三棱柱侧棱与底面垂直,因此可得![]() ,由此得
,由此得![]() ,从而得线面垂直;(Ⅱ)要求
,从而得线面垂直;(Ⅱ)要求![]() 与平面
与平面![]() 所成的角,一般要作出线面角,实际上要作出
所成的角,一般要作出线面角,实际上要作出![]() 在平面
在平面![]() 内的射影,即过
内的射影,即过![]() 作平面
作平面![]() 的垂线,由(Ⅰ)知
的垂线,由(Ⅰ)知![]() 平面
平面![]() ,因此想到平移
,因此想到平移![]() 到
到![]() 点位置,为此取
点位置,为此取![]() 的中点
的中点![]() ,连
,连![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可得
,可得![]() ,即
,即![]() 平面
平面![]() ,所以
,所以![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,解相应直角三角形可得.
所成的角,解相应直角三角形可得.
试题解析:
(Ⅰ)证明:因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ;
;

(Ⅱ)取![]() 的中点
的中点![]() ,连
,连![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
由已知得,![]() ,
,![]() ,
,
所以![]() .-
.-


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1=![]() ,公比q=
,公比q=![]() 的等比数列,设
的等比数列,设![]() ,数列
,数列![]() 满足cn=an·bn.
满足cn=an·bn.
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤![]() m2+m-1对一切正整数n恒成立,求实数m的取值范围.
m2+m-1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=cos2x的图象,只需将y=cos(2x+ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中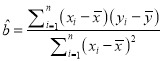 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0, ![]() ).
).
(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 令Tn= ![]() ,称Tn为数列a1 , a2 , …,an的“理想数”,已知数列a1 , a2 , …,a502的“理想数”为2012,那么数列2,a1 , a2 , …,a502的“理想数”为( )
,称Tn为数列a1 , a2 , …,an的“理想数”,已知数列a1 , a2 , …,a502的“理想数”为2012,那么数列2,a1 , a2 , …,a502的“理想数”为( )
A.2010
B.2011
C.2012
D.2013
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com