练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题正确的是（ ）
    A.若 ，则 =0
    B.若 = ，则 =
    C.若 ∥ ， ∥ ，则 ∥
    D.若 与 是单位向量，则 =1

    【答案】A
    【解析】解：对于A．若| |=| ﹣ |，则（ ）2=（ ）2 ，
    即 +2 = ﹣2 ，则有 =0，则A正确；
    对于B．若 = ，则 ，则B错误；
    对于C．若 ∥ ， ∥ ，则 也成立，则C错误；
    对于D．若 与 是单位向量，则 =| || |cos＜ ＞=cos＜ ＞，
    则D错误．
    故选A．
    由平方法和向量的数量积的性质，即可判断A；由向量数量积的性质，即可判断B；
    由零向量与任何向量共线，即可判断C；运用单位向量的定义及数量积的定义，即可判断D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】椭圆+=1的左、右焦点分别为F1，F2，一条直线经过点F1与椭圆交于A，B两点．

    （1）求△ABF2的周长；

    （2）若的倾斜角为，求弦长|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一个几何体的三视图如图所示.

    （1）求此几何体的表面积；

    （2）如果点在正视图中所示位置：为所在线段中点，为顶点，求在几何体表面上，从点到点的最短路径的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=sin（ωx+）（ω＞0，0≤≤π）为偶函数，其图象上相邻的两个最高点之间的距离为2π．
    （1）求f（x）的解析式；
    （2）若 ，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，点P，G分别是AD,EF的中点，已知平面ABC，AD=EF=3，DE=DF=2．

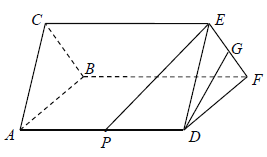
    （Ⅰ）求证：DG⊥平面BCEF；

    （Ⅱ）求PE与平面BCEF 所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.

    已知从全部105人中随机抽取1人为优秀的概率为.

    （1）请完成上面的列联表：若按的可靠性要求，根据列联表的数据，能否认为“成绩与班级有关系”；

    （2）若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号.试求抽到10号的概率.

    附：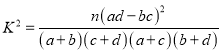

    查看答案和解析>>

    科目：高中数学 来源： 题型：

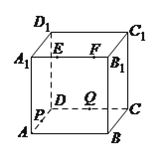
    【题目】如图，正方体的棱长为，动点、在棱上，动点，分别在棱，上，若，，，（，，大于零），则四面体的体积（ ）．

    A. 与，，都有关 B. 与有关，与，无关

    C. 与有关，与，无关 D. 与有关，与，无关

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂有4台大型机器，在一个月中，一台机器至多出现1次故障，且每台机器是否出现故障是相互独立的，出现故障时需1名工人进行维修，每台机器出现故障需要维修的概率为.

    (1)若出现故障的机器台数为，求的分布列；

    (2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%？

    (3)已知一名工人每月只有维修1台机器的能力，每月需支付给每位工人1万元的工资，每台机器不出现故障或出现故障能及时维修，就使该厂产生5万元的利润，否则将不产生利润，若该厂现有2名工人，求该厂每月获利的均值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将五个1，五个2，五个3，五个4，五个5共25个数填入一个5行5列的表格内（每格填入一个数），使得同一行中任何两数之差的绝对值不超过2，考查每行中五个数之和，记这五个和的最小值为，则的最大值为（ ）

    A. B. 9 C. 10 D. 11

    查看答案和解析>>

    同步练习册答案