
����Ŀ��ij����4̨���ͻ�������һ�����У�һ̨�����������1�ι��ϣ���ÿ̨�����Ƿ���ֹ�����������ģ����ֹ���ʱ��1�����˽���ά�ޣ�ÿ̨�������ֹ�����Ҫά�ĸ���Ϊ![]() .
.
(1)�����ֹ��ϵĻ���̨��Ϊ![]() ����
����![]() �ķֲ��У�
�ķֲ��У�
(2) �ó������ж��������˲��ܱ�֤ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά�ĸ��ʲ�����90%��
(3)��֪һ������ÿ��ֻ��ά��1̨������������ÿ����֧����ÿλ����1��Ԫ�Ĺ��ʣ�ÿ̨���������ֹ��ϻ���ֹ����ܼ�ʱά�ޣ���ʹ�ó�����5��Ԫ�������������������ó�����2�����ˣ���ó�ÿ�»����ľ�ֵ.
���𰸡�(1) ![]() ;(2)
;(2) ![]() ��
��
�������������������1���������������ж�������������Ӷ���ֲ��������ö���ֲ��ĸ��ʹ�ʽ���ÿ��������Ӧ�ĸ��ʣ����б��õ��ֲ�������2�����û����¼�������һ�������ĸ��ʹ�ʽ������⣻��3���г�������������п���ȡֵ�����ö�Ӧ��ϵ�õ�ÿ�������ĸ��ʣ��б��õ��ֲ��У������õ�����ֵ.
�����������1��һ̨���������Ƿ���ֹ��Ͽɿ���һ��ʵ�飬��һ�������У��������ֹ�����Ϊ![]() �����¼�
�����¼�![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ���ó���4̨�������൱��4�ζ����ظ����飬����ֹ��ϵĻ���̨��Ϊ
���ó���4̨�������൱��4�ζ����ظ����飬����ֹ��ϵĻ���̨��Ϊ![]() ����
����![]() ��
��
![]() ��
�� ![]() ,
,
![]() ��
�� ![]()
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
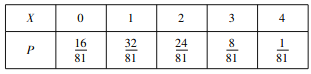
��2����ó���![]() �����ˣ���ÿ̨�������κ�ʱ��ͬʱ���ֹ��ϼ�ʱ����ά�ޡ�Ϊ
�����ˣ���ÿ̨�������κ�ʱ��ͬʱ���ֹ��ϼ�ʱ����ά�ޡ�Ϊ![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() �������¼��ĺ��¼�����
�������¼��ĺ��¼�����
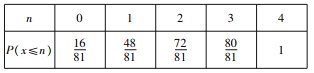
![]() %
%![]() ,
,
![]() ����Ҫ3�����ˣ����ܱ�֤ÿ̨�������κ�ʱ��ͬʱ���ֹ����ܼ�ʱ����ά�ĸ��ʲ�����90%.
����Ҫ3�����ˣ����ܱ�֤ÿ̨�������κ�ʱ��ͬʱ���ֹ����ܼ�ʱ����ά�ĸ��ʲ�����90%.
��3����ó�����Ϊ![]() ��Ԫ����
��Ԫ����![]() �����п���ȡֵΪ��
�����п���ȡֵΪ�� ![]()
![]() ��
��
![]() ��
��
![]() ��
��
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
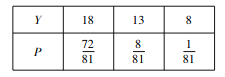
��![]() ��
��
�ʸó������ľ�ֵΪ![]() .
.


 �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���洬��λ�ڵ���A����ƫ��60�㷽���B�������뵺��A���12����洬����10����/Сʱ���ٶȴӵ���A���������������У����洬��ͬʱ��B�������ر�ƫ�����ķ������洬�ң��պ���2Сʱ�ϣ� 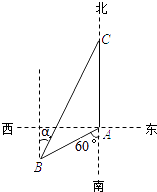
��1�����洬���ٶȣ�
��2����sin����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.�� ![]() ����
���� ![]()
![]() =0
=0
B.�� ![]()
![]() =
= ![]()
![]() ����
���� ![]() =
= ![]()
C.�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]()
D.�� ![]() ��
�� ![]() �ǵ�λ��������
�ǵ�λ�������� ![]()
![]() =1
=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
����![]() ����С�����ں͵����������䣻
����С�����ں͵����������䣻
������֪a��b��c�ǡ�ABC���߳�����f��C��=2����ABC�����S=![]() ��c=7�����C��a��b��ֵ��
��c=7�����C��a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC������������F1����2��0����F2��2��0��������ԲC������A��0�� ![]() ����
����
��1������ԲC�ı����̣�
��2��������ԲC����F1����2��0����б��Ϊ1��ֱ��l����ԲC����P��Q���㣬���߶�PQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=sin2x��x��R��ͼ�������еĵ�����ƽ�� ![]() ����λ���ȣ�����ͼ��ĺ�������ʽΪ ��
����λ���ȣ�����ͼ��ĺ�������ʽΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=sinxcosx�� f��x����ͼ������ƽ�� ![]() ��0���գ��У� ����λ���õ�y=g��x��ͼ����g��x����һ���Գ�����ֱ��x=
��0���գ��У� ����λ���õ�y=g��x��ͼ����g��x����һ���Գ�����ֱ��x= ![]() ��
��
��1����գ�
��2������y=g��x���ĵ��������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵΪ�˽�����ij���ŶԱ���ҵְ���ķ���������������50��ְ����������50��ְ���Ըò��ŵ����֣�����Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���������������ݷ�������Ϊ[40��50]��[50��60]������[80��90]��[90��100] 
��1����Ƶ�ʷֲ�ͼ��a��ֵ��
��2�����Ƹ���ҵ��ְ���Ըò������ֲ�����80�ĸ��ʣ�
��3����������[40��60]���ܷ�ְ���У������ȡ2�ˣ����2�����ֶ���[40��50]�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() =��cosx����
=��cosx���� ![]() ����
���� ![]() =��sinx+cosx��1����f��x��=
=��sinx+cosx��1����f��x��= ![]()
![]() ��
��
��1����0������ ![]() ��sin��=
��sin��= ![]() ����f��������ֵ��
����f��������ֵ��
��2������f��x������С�����ڼ������������䣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com