
【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0, ![]() ).
).
(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长.
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
|
|
|
|
|
|
|
|
|
|
(1)请画出上表数据的散点图;并指出![]() 是否线性相关;
是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
![]() ;
;
(3)已知该厂技术改造前![]() 吨甲产品能耗为
吨甲产品能耗为![]() 吨标准煤,试根据求出的线性回归方程,预测生产
吨标准煤,试根据求出的线性回归方程,预测生产![]() 吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,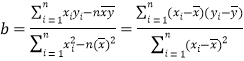 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱中![]() ,点P,G分别是AD,EF的中点,已知
,点P,G分别是AD,EF的中点,已知![]() 平面ABC,AD=EF=3,DE=DF=2.
平面ABC,AD=EF=3,DE=DF=2.
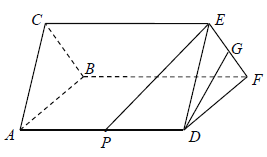
(Ⅰ)求证:DG⊥平面BCEF;
(Ⅱ)求PE与平面BCEF 所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 、
、![]() 在棱
在棱![]() 上,动点
上,动点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上,若
上,若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 大于零),则四面体
大于零),则四面体![]() 的体积( ).
的体积( ).
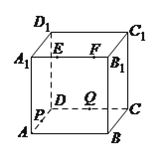
A. 与![]() ,
,![]() ,
,![]() 都有关 B. 与
都有关 B. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
C. 与![]() 有关,与
有关,与![]() ,
,![]() 无关 D. 与
无关 D. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)若出现故障的机器台数为![]() ,求
,求![]() 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于![]() 为合格品,小于
为合格品,小于![]() 为次品.现随机抽取这种芯片共
为次品.现随机抽取这种芯片共![]() 件进行检测,检测结果统计如表:
件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
芯片数量(件) |
|
|
|
|
|
已知生产一件芯片,若是合格品可盈利![]() 元,若是次品则亏损
元,若是次品则亏损![]() 元.
元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产![]() 件芯片所获得的利润不少于
件芯片所获得的利润不少于![]() 元的概率.
元的概率.
(Ⅱ)记![]() 为生产
为生产![]() 件芯片所得的总利润,求随机变量
件芯片所得的总利润,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市共有初中学生270000人,其中初一年级,初二年级,初三年级学生人数分别为99000,90000,81000,为了解该市学生参加“开放性科学实验活动”的意向,现采用分层抽样的方法从中抽取一个容量为3000的样本,那么应该抽取初三年级的人数为( )
A.800
B.900
C.1000
D.1100
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com