
分析 (1)利用零点法,去除绝对值符号,解相应的不等式,最后综合讨论结果,可得答案;
(2)先利用绝对值三角不等式求f(x)的最小值,进而利用零点分段法,可得实数a的取值范围.
解答 解:(1)当x<1时,不等式f(x)≤4可化为:4-2x≤4,解得:x≥0,
∴0≤x<1;
当1≤x≤3时,不等式f(x)≤4可化为:2≤4,恒成立;
当x>3时,不等式f(x)≤4可化为:2x-4≤4,解得:x≤4,
∴3<x≤4,
综上可得:原不等式的解集为:[0,4];
(2)∵f(x)=|x-1|+|x-3|=|1-x|+|x-3|≥|1-x+x-3|=2.
若对?x∈R,a2-|a|≤f(x),
则a2-|a|≤2,
当a≥0时,即a2-a-2≤0,解得:-1≤a≤2,
∴0≤a≤2,
当a<0时,即a2+a-2≤0,解得:-2≤a≤1,
∴-2≤a<0,
综上可得实数a的取值范围为:[-2,2].
点评 本题考查的知识点是绝对值不等式的解法,绝对值三角不等式,零点分段法,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{2-\sqrt{2}}}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
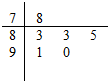 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:| A. | ①② | B. | ③④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-$\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{6}$$-\sqrt{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | b<c<a | C. | a<b<c | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com