
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)先求导数,再根据导数几何意义得切线斜率,根据点斜式得切线方程,求出与坐标轴交点坐标,最后根据三角形面积公式得结果;
(2)解法一:利用导数研究,得到函数![]() 得导函数
得导函数![]() 的单调递增,当a=1时由
的单调递增,当a=1时由![]() 得
得![]() ,符合题意;当a>1时,可证
,符合题意;当a>1时,可证![]() ,从而
,从而![]() 存在零点
存在零点![]() ,使得
,使得![]() ,得到
,得到![]() ,利用零点的条件,结合指数对数的运算化简后,利用基本不等式可以证得
,利用零点的条件,结合指数对数的运算化简后,利用基本不等式可以证得![]() 恒成立;当
恒成立;当![]() 时,研究
时,研究![]() .即可得到不符合题意.综合可得a的取值范围.
.即可得到不符合题意.综合可得a的取值范围.
解法二:利用指数对数的运算可将![]() ,
,
令![]() ,上述不等式等价于
,上述不等式等价于![]() ,注意到
,注意到![]() 的单调性,进一步等价转化为
的单调性,进一步等价转化为![]() ,令
,令![]() ,利用导数求得
,利用导数求得![]() ,进而根据不等式恒成立的意义得到关于a的对数不等式,解得a的取值范围.
,进而根据不等式恒成立的意义得到关于a的对数不等式,解得a的取值范围.
(1)![]() ,
,![]() ,
,![]() .
.
![]() ,∴切点坐标为(1,1+e),
,∴切点坐标为(1,1+e),
∴函数f(x)在点(1,f(1)处的切线方程为![]() ,即
,即![]() ,
,
![]() 切线与坐标轴交点坐标分别为
切线与坐标轴交点坐标分别为![]() ,
,
∴所求三角形面积为![]() ;
;
(2)解法一:![]() ,
,
![]() ,且
,且![]() .
.
设![]() ,则
,则![]()
∴g(x)在![]() 上单调递增,即
上单调递增,即![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() 成立.
成立.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
∴存在唯一![]() ,使得
,使得![]() ,且当
,且当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,![]() ,
,![]() ,
,
因此![]()
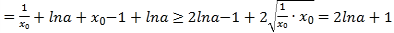 >1,
>1,
∴![]() ∴
∴![]() 恒成立;
恒成立;
当![]() 时,
时, ![]() ∴
∴![]() 不是恒成立.
不是恒成立.
综上所述,实数a的取值范围是[1,+∞).
解法二:![]() 等价于
等价于
![]() ,
,
令![]() ,上述不等式等价于
,上述不等式等价于![]() ,
,
显然![]() 为单调增函数,∴又等价于
为单调增函数,∴又等价于![]() ,即
,即![]() ,
,
令![]() ,则
,则![]()
在![]() 上h’(x)>0,h(x)单调递增;在(1,+∞)上h’(x)<0,h(x)单调递减,
上h’(x)>0,h(x)单调递增;在(1,+∞)上h’(x)<0,h(x)单调递减,
∴![]() ,
,
![]() ,∴a的取值范围是[1,+∞).
,∴a的取值范围是[1,+∞).


科目:高中数学 来源: 题型:
【题目】为培养学生对传统文化的兴趣,某校从理科甲班抽取60人,从文科乙班抽取50人参加传统文化知识竞赛.
(1)根据题目条件完成下边![]() 列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 20 | ||
总计 | 60 |
(2)现已知![]() ,
,![]() ,
,![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
,![]() ,
,![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
,![]() ,
,![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附: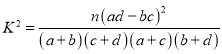 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A≠0,ω>0,![]() <φ<
<φ<![]() )的图象关于直线
)的图象关于直线![]() 对称,它的最小正周期为π,则( )
对称,它的最小正周期为π,则( )
A. f(x)的图象过点(0,![]() ) B. f(x)在
) B. f(x)在![]() 上是减函数
上是减函数
C. f(x)的一个对称中心是![]() D. f(x)的一个对称中心是
D. f(x)的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=![]() ,
,![]() ,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
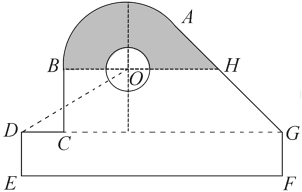
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《周髀算经》中,把圆及其内接正方形称为圆方图,把正方形及其内切圆称为方圆图.圆方图和方圆图在我国古代的设计和建筑领域有着广泛的应用.山西应县木塔是我国现存最古老、最高大的纯木结构楼阁式建筑,它的正面图如下图所示.以该木塔底层的边![]() 作正方形,以点
作正方形,以点![]() 或点
或点![]() 为圆心,以这个正方形的对角线为半径作圆,会发现塔的高度正好跟此对角线长度相等.以该木塔底层的边
为圆心,以这个正方形的对角线为半径作圆,会发现塔的高度正好跟此对角线长度相等.以该木塔底层的边![]() 作正方形,会发现该正方形与其内切圆的一个切点
作正方形,会发现该正方形与其内切圆的一个切点![]() 正好位于塔身和塔顶的分界线上.经测量发现,木塔底层的边
正好位于塔身和塔顶的分界线上.经测量发现,木塔底层的边![]() 不少于47.5米,塔顶
不少于47.5米,塔顶![]() 到点
到点![]() 的距离不超过19.9米,则该木塔的高度可能是(参考数据:
的距离不超过19.9米,则该木塔的高度可能是(参考数据:![]() )( )
)( )
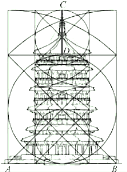
A.66.1米B.67.3米C.68.5米D.69.0米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,左右项点分别为
,左右项点分别为![]() ,点
,点![]() 是
是![]() 上的动点.
上的动点.
(1)若点![]() 在第一象限, 且
在第一象限, 且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)点![]() 与
与![]() 不重合,直线
不重合,直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点,求证:
两点,求证: ![]() ;
;
(3)若点![]() 在左支上,是否存在实数
在左支上,是否存在实数![]() ,使得
,使得![]() 到直线
到直线![]() 的距离与
的距离与![]() 之比为定值?若存在,求出
之比为定值?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,
,![]() ),
),![]() ,且函数
,且函数![]() 图像上的任意两条对称轴之间距离的最小值是
图像上的任意两条对称轴之间距离的最小值是![]() .
.
(1)求![]() 的值和
的值和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图像,求函数
的图像,求函数![]() 在
在![]() 上的最值,并求取得最值时的
上的最值,并求取得最值时的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com