
| 喜欢歌舞类节目 | 不喜欢歌舞类节目 | 合计 | |
| 男性 | |||
| 女性 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0,10 | 0.05 | 0.025 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 |
分析 (1)利用列举法,确定基本事件的个数,即可求观众A和B至少有1人被抽中的概率.
(2)根据图表可得2×2列表,计算K2,与临界值比较,即可得出结论.
解答 解:(1)从5名观众中任取2名,共有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE10种不同的取法,A,B至少有1人被抽中共有7种,所以$P=\frac{7}{10}$.
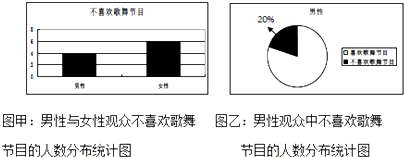
(2)男性不喜欢歌舞节目的共有4人,所以男性共有$\frac{4}{20%}$=20人,
其中喜欢歌舞节目的有20-4=16人,
女性不喜欢歌舞节目的共有6人,喜欢歌舞节目的有100-20-6=74人,∴2×2列联表如下图:
| 喜欢歌舞类节目 | 不喜欢歌舞类目 | 合计 | |
| 男性 | 16 | 4 | 20 |
| 女性 | 74 | 6 | 80 |
| 合计 | 90 | 10 | 100 |
点评 本题考查概率的计算,考查2×2列表、独立性检验知识,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
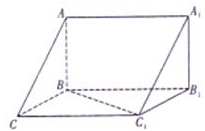 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,$B{C_1}=\sqrt{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,$B{C_1}=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{ln3}{6}$]∪[$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | (0,$\frac{ln3}{6}$] | C. | (0,e) | D. | [$\frac{ln3}{6}$,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 感染 | 未感染 | 总计 | |
| 服用 | 10 | 40 | 50 |
| 未服用 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(k2≥k) | 0.10 | 0.05 | 0.025 |
| K | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com