
已知数列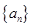 中,
中,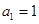 ,
, ,数列
,数列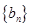 中,
中, ,且点
,且点 在直线
在直线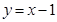 上.
上.
(Ⅰ)求数列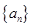 的通项公式;
的通项公式;
(Ⅱ)求数列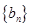 的通项公式;
的通项公式;
(Ⅲ)若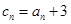 ,求数列
,求数列 的前项和
的前项和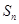 .
.
(Ⅰ) 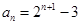 ;(Ⅱ)
;(Ⅱ)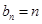 ;(Ⅲ)
;(Ⅲ)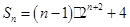 .
.
解析试题分析:(Ⅰ) 由已知可构造数列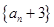 ,并证明其为等比数列,先求出数列
,并证明其为等比数列,先求出数列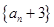 的通项公式,再求数列
的通项公式,再求数列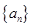 的通项公式(一般形如
的通项公式(一般形如 的递推关系,可先构造等比数列
的递推关系,可先构造等比数列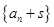 ,其公比
,其公比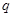 与常数
与常数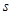 ,可由
,可由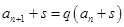 与所给等式
与所给等式 进行比较求得);(Ⅱ)将点
进行比较求得);(Ⅱ)将点 代入直线方程
代入直线方程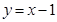 ,可得到数列
,可得到数列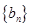 中
中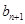 与
与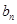 的关系式,从而发现
的关系式,从而发现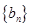 为等差数列,即可求出数列
为等差数列,即可求出数列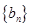 的通项公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得数列
的通项公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得数列 的通项公式,观察
的通项公式,观察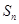 中各项关系,可用错位相减法来求出
中各项关系,可用错位相减法来求出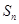 (错位相减法是求数列前项
(错位相减法是求数列前项 和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
试题解析:(Ⅰ)由 得
得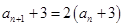
所以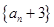 是首项为
是首项为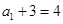 ,公比为2的等比数列.
,公比为2的等比数列.
所以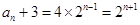 ,故
,故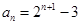
(Ⅱ)因为 在直线
在直线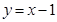 上,
上,
所以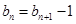 即
即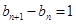 又
又
故数列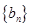 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
所以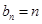
(Ⅲ)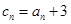 =
=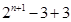 =
=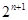 故
故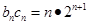
所以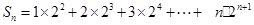
故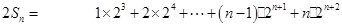
相减得
所以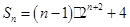
考点:1.等比数列;2.等差数列;3.数列前项 和求法.
和求法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知数列{an}是首项为-1,公差d  0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
(1)求{an}的通项公式;
(2)若Cn=an·bn,求数列{Cn}的前n项和Sn。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现在市面上有普通型汽车(以汽油为燃料)和电动型汽车两种。某品牌普通型汽车车价为12万元,第一年汽油的消费为6000元,随着汽油价格的不断上升,汽油的消费每年以20%的速度增长。其它费用(保险及维修费用等)第一年为5000元,以后每年递增2000元。而电动汽车由于节能环保,越来越受到社会认可。某品牌电动车在某市上市,车价为25万元,购买时一次性享受国家补贴价6万元和该市市政府补贴价4万元。电动汽车动力不靠燃油,而靠电池。电动车使用的普通锂电池平均使用寿命大约两年(也即两年需更换电池一次),电池价格为1万元,电动汽车的其它费用每年约为5000元。
求使用 年,普通型汽车的总耗资费
年,普通型汽车的总耗资费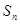 (万元)的表达式
(万元)的表达式
(总耗资费=车价+汽油费+其它费用)
比较两种汽车各使用10年的总耗资费用
(参考数据: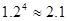
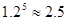
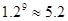
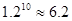 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列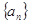 中,
中,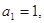 且点
且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)若函数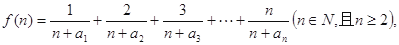 求函数
求函数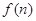 的最小值;
的最小值;
(3)设 表示数列
表示数列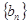 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式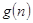 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立?若存在,写出
恒成立?若存在,写出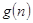 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com