
分析 (1)令F(x)=f(x)-x=$\frac{1}{2}ln(2x)+\frac{1}{2}-x$,则${F}^{'}(x)=\frac{1-2x}{2x}$,利用导数性质能证明$x>\frac{1}{2}$时,f(x)<x.
(2)利用数学归纳法能证明$\frac{1}{2}<{a_n}≤1$(n∈N*).
(3)推导出$\frac{1}{2}<{a}_{n+1}=f({a}_{n})<{a}_{n}≤1$,从而${a}_{i+1}<\frac{{a}_{i}+{a}_{i+1}}{2}$,进而(ai-ai+1)ai+1<$\frac{1}{2}({{a}_{i}}^{2}-{{a}_{i+1}}^{2})$,由此能证明$\sum_{i=1}^n{({a_i}-{a_{i+1}})}•{a_{i+1}}<\frac{3}{8}$(n∈N*).
解答 证明:(1)令F(x)=f(x)-x=$\frac{1}{2}ln(2x)+\frac{1}{2}-x$,
则${F}^{'}(x)=\frac{1-2x}{2x}$,又x>$\frac{1}{2}$,∴F′(x)<0,
∴F(x)在($\frac{1}{2}$,+∞)为减函数,
∴F(x)<F($\frac{1}{2}$)=0,
∴$x>\frac{1}{2}$时,f(x)<x.
(2)①当n=1时,a1=1,$\frac{1}{2}<{a}_{1}≤1$成立;
②假设n=k(k∈N*)时,$\frac{1}{2}<{a}_{k}≤1$,
当n=k+1(k∈N*)时,${a}_{k+1}=f({a}_{k})=\frac{1}{2}ln(2{a}_{k})+\frac{1}{2}$,
根据归纳假设$\frac{1}{2}<{a}_{k}≤1$,
由①得:$\frac{1}{2}ln(2×\frac{1}{2})+\frac{1}{2}<\frac{1}{2}ln(2{a}_{k})+\frac{1}{2}≤\frac{1}{2}ln(2×1)+\frac{1}{2}$,
∴$\frac{1}{2}<{a}_{k+1}≤1$,即n=k+1时命题成立.
综上所述,$\frac{1}{2}<{a_n}≤1$(n∈N*).
(3)由$\frac{1}{2}<{a_n}≤1$(n∈N*),${a}_{n+1}=f({a}_{n}),x>\frac{1}{2},f(x)<x$,
得$\frac{1}{2}<{a}_{n+1}=f({a}_{n})<{a}_{n}≤1$,
∴${a}_{i+1}<\frac{{a}_{i}+{a}_{i+1}}{2}$,
∵ai-ai+1>0,
∴(ai-ai+1)ai+1<(ai-ai+1)•$\frac{{a}_{i}+{a}_{i+1}}{2}$=$\frac{1}{2}({{a}_{i}}^{2}-{{a}_{i+1}}^{2})$,
∴$\sum_{i=1}^{n}({a}_{i}-{a}_{i+1})•{a}_{i+1}$<$\frac{1}{2}({{a}_{1}}^{2}+{{a}_{2}}^{2}+…+{{a}_{n}}^{2}-{{a}_{n+1}}^{2})$
=$\frac{1}{2}({{a}_{1}}^{2}-{{a}_{n+1}}^{2})=\frac{1}{2}(1-{{a}_{n+1}}^{2})$<$\frac{1}{2}(1-\frac{1}{{2}^{2}})$=$\frac{3}{8}$.
∴$\sum_{i=1}^n{({a_i}-{a_{i+1}})}•{a_{i+1}}<\frac{3}{8}$(n∈N*).
点评 本题考查不等式的证明,是中档题,解题时要认真审题,注意导数性质、数列性质、放缩法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
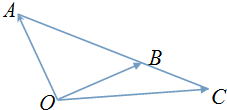
| A. | $\overrightarrow{c}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$ | B. | $\overrightarrow{c}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{c}$=-$\overrightarrow{a}$+2$\overrightarrow{b}$ | D. | $\overrightarrow{c}$=$\overrightarrow{a}$+2$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | -1<a<0 | C. | a<1 | D. | 0<a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com