
已知圆C: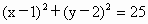 ,直线l:(2m+1)x+(m+1)y-7m-4=0(mÎ
R),
,直线l:(2m+1)x+(m+1)y-7m-4=0(mÎ
R),
(1)证明不论m为何实数时,直线l和圆恒交两点;
(2)求直线l被圆C截得的弦长最小时l的方程.
|
直线 l恒过定点,只需证明定点;在圆内即可.(1) 证明:直线l的方程为x+y-4+m(2x+y-7)=0.由 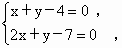 得 得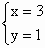
∴ l恒过定点A(3,1).∵圆心 C(1,2),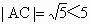 (半径), (半径),
∴点 A在圆C内,从而直线l恒与圆C相交于两点.(2) 解:弦长最小时,l⊥AC.由 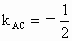 ,∴ ,∴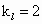 . .
所以 l的方程为2x-y-5=0.点拨: (1)直线过定点问题的解题思路是:将含有待定系数的项放在一起,不含有待定系数的项放在一起,即化为直线系方程,通过解两真线的方程组成的方程组,便可证得直线系经过两条直线的交点;同时得到直线经过的定点.(2) 运用几何法解直线与圆有关的问题会使问题直观易懂,使计算简便. |


科目:高中数学 来源:2012-2013学年四川省雅安中学高二10月月考理科数学试卷(带解析) 题型:解答题
已知圆C: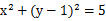 ,直线L:
,直线L: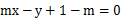
(1)求证:对m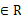 ,直线L与圆C总有两个交点;
,直线L与圆C总有两个交点;
(2)设直线L与圆C交于点A、B,若|AB|=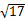 ,求直线L的倾斜角;
,求直线L的倾斜角;
(3)设直线L与圆C交于A、B,若定点P(1,1)满足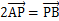 ,求此时直线L的方程.
,求此时直线L的方程.
查看答案和解析>>
科目:高中数学 来源:西南师大附中2010届高三第五次月考(数学理)试题 题型:解答题
已知圆C: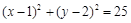 ,直线l:
,直线l: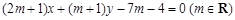 .
.
(1)证明:不论m取什么实数时,直线l与圆恒交于两点;
(2)求直线l被圆C截得的线段的最短长度以及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com