
分析 函数f(x)在(-∞,+∞)上是具有单调性,需要对m分类讨论,当m>1,m<-1,m=±1、0,-1<m<0,0<m<1分别判断分段函数的单调性.
解答 解:令 h(x)=mx2+1,x≥0;g(x)=(m2-1)2x,x<0;
①当 m>1时,要使得f(x)在(-∞,+∞)上是具有单调性,
即要满足m2-1≤1⇒-$\sqrt{2}$≤m≤$\sqrt{2}$
故:1<m≤$\sqrt{2}$;
②当 m<-1时,h(x)在x≥0上递减,g(x)在x<0上递增,
所以,f(x)在R上不具有单调性,不符合题意;
③当 m=±1时,g(x)=0;当m=0时,h(x)=1;
所以,f(x)在R上不具有单调性,不符合题意;
④当-1<m<0 时,h(x)在x≥0上递减,g(x)在x<0上递减,
对于任意的x≥0,g(x)<0;当x→0时,h(x)>0;
所以,f(x)在R上不具有单调性,不符合题意;
⑤当0<m<1时,h(x)在x≥0上递增,g(x)在x<0上递减;
所以,f(x)在R上不具有单调性,不符合题意;
故答案为:(1,$\sqrt{2}$]
点评 本题主要考查了分段函数的单调性,二次函数与指数函数、以及分类讨论知识点,属基础题.


科目:高中数学 来源: 题型:解答题
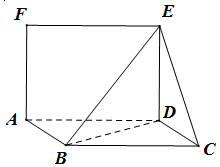 在平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,矩形ADEF中DE=1,且面ADEF⊥面ABCD.
在平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,矩形ADEF中DE=1,且面ADEF⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},+∞)$ | B. | $[\frac{1}{2},+∞)$ | C. | $(\frac{1}{4},+∞)$ | D. | $[\frac{1}{4},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{15}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com