
分析 (Ⅰ)利用列举法写出数列{cn},易得集合A;
(Ⅱ)由题设,对n≥3,cn-2,cn-1都是奇数,所以cn-1+cn-2是偶数.从而cn-1+cn-2的最大奇约数${c_n}≤\frac{{{c_{n-1}}+{c_{n-2}}}}{2}$,结合不等式的性质进行解答;
(Ⅲ)有限集是指元素的个数是有限个的集合,从而确定答案.
解答 解:(Ⅰ)数列{cn}为:9,15,3,9,3,3,3,….
故集合A={9,15,3}.
(Ⅱ)证明:由题设,对n≥3,cn-2,cn-1都是奇数,所以cn-1+cn-2是偶数.
从而cn-1+cn-2的最大奇约数${c_n}≤\frac{{{c_{n-1}}+{c_{n-2}}}}{2}$,
所以cn≤max{cn-1,cn-2},当且仅当cn-1=cn-2时等号成立.
所以,对k≥1有c2k+1≤max{c2k,c2k-1}=dk,
且c2k+2≤max{c2k+1,c2k}≤max{dk,dk}=dk.
所以dk+1=max{c2k+2,c2k+1}≤dk,当且仅当c2k=c2k-1时等号成立.
(Ⅲ)由(Ⅱ)知,当n≥3时,有cn≤max{cn-1,cn-2}.
所以对n≥3,有cn≤max{c1,c2}=max{a,b}.
又cn是正奇数,且不超过max{a,b}的正奇数是有限的,
所以数列{cn}中的不同项是有限的.
所以集合A是有限集.
集合A中的最小数是a,b的最大公约数.
点评 本题考查了集合的表示方法,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
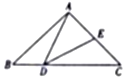 如图所示,在△ABC中,点D为BC边上一点,且BD=1,E为AC的中点,AE=$\frac{3}{2}$,cosB=$\frac{{2\sqrt{7}}}{7}$,∠ADB=$\frac{2π}{3}$.
如图所示,在△ABC中,点D为BC边上一点,且BD=1,E为AC的中点,AE=$\frac{3}{2}$,cosB=$\frac{{2\sqrt{7}}}{7}$,∠ADB=$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
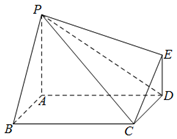 如图,四边形ABCD为矩形,PA⊥平面ABCD,DE∥PA.
如图,四边形ABCD为矩形,PA⊥平面ABCD,DE∥PA.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com