Question

7．某班一次数学测试成绩的茎叶图（茎上数代表十位，叶上数带表个位）如图1示
（1）以10为组距，图2给定的坐标系中画出该班成绩的频率分布直方图；
（2）用分层抽样的方法抽取一个容量为8的样本，在样本中从分数在[60，80）之间的试卷中任取2份分析学生失分情况，求所抽取的2份试卷中至少有一份分数在[60，70）概率．

Answer 1

分析 （1）频率分布直方图中，求出分数在各分数段内的频率，即可求出矩形的高，画出图象即可；
（2）由题意，各分数段的人数分别为1，2，3，1，1，然后列出基本事件空间包含的基本事件，以及所抽取的2份试卷中至少有一份分数在[60，70）的基本事件，最后将包含事件的个数求出题目比值即可．

解答 解：（1）分数在[50，60）内的频率为$\frac{4}{32}$=0.125；分数在[60，70）内的频率为0.25；分数在[70，80）内的频率为0.375；分数在[80，90）内的频率为0.125；分数在[90，100）内的频率为0.125．频率分布直方图如图所示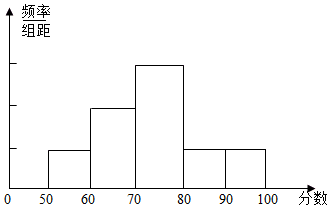
（2）由题意，各分数段的人数分别为1，2，3，1，1，在[60，80）之间的人数为5，任取2份有C₅²=10种情况，所抽取的2份试卷中至少有一份分数在[60，70）的基本事件有C₂¹C₃¹+C₂²=7种情况，所以所抽取的2份试卷中至少有一份分数在[60，70）概率为0.7．

点评 本题主要考查了频率及频率分布直方图，以及概率的有关问题，考查运用统计知识解决简单实际问题的能力，数据处理能力和运用意识．