
| A. | (-1,+∞) | B. | (-∞,-1] | C. | (1,+∞) | D. | (-∞,1] |
分析 数列b3,b4,b5,…是“减差数列”,可得n≥3时,bn+bn+2<2bn+1,代入化简即可得出.
解答 解:∵数列b3,b4,b5,…是“减差数列”,∴n≥3时,bn+bn+2<2bn+1,
∴2t-$\frac{tn-1}{{2}^{n-1}}$+2t-$\frac{t(n+2)-1}{{2}^{n+1}}$<2$(2t-\frac{t(n+1)-1}{{2}^{n}})$,
化为:4(tn-1)+t(n+2)-1>4t(n+1)-4,
∴t$>\frac{1}{n-2}$,∵n≥3,∴$\frac{1}{n-2}$≤1,
∴t>1.
∴实数t的取值范围是(1,+∞).
故选:C.
点评 本题考查了新定义“减差数列”、不等式的解法,考查了推理能力与计算能力,属于中档题.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:选择题
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
| A. | y=12+3sin$\frac{πt}{6}$,t∈[0,24] | B. | y=12+3sin($\frac{πt}{6}$+π),t∈[0,24] | ||
| C. | y=12+3sin$\frac{πt}{12}$,t∈[0,24] | D. | y=12+3sin($\frac{πt}{12}$+$\frac{π}{2}$),t∈[0,24] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{12}{5}$ | B. | $\frac{12}{5}$ | C. | ±$\frac{12}{5}$ | D. | ±$\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
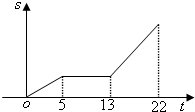 某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法:
某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com