
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 写出特称命题的否定判断①;写出原命题的逆否命题判断②;由函数为偶函数求得a值判断③;利用基本不等式求得最值判断④;由函数的性质结合已知求得f($\frac{3}{2}$)的值判断⑤.
解答 解:①命题“?x∈R,使得x2+1>3x”的否定是“?x∈R,都有x2+1≤3x”,故①错误;
②命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1”,故②正确;
③若函数f(x)=(x+1)(x+a)为偶函数,则f(-x)-f(x)=(-x+1)(-x+a)-(x+1)(x+a)=-(a+1)x=0恒成立,
∴a=-1,故③正确;
④若x>0,y>0且2x+y=1,则$\frac{1}{x}$+$\frac{1}{y}$=$(\frac{1}{x}+\frac{1}{y})(2x+y)=3+\frac{y}{x}+\frac{2x}{y}$$≥3+2\sqrt{2}$,当且仅当$\left\{\begin{array}{l}{2x+y=1}\\{y=\sqrt{2}x}\end{array}\right.$,即x=1-$\frac{\sqrt{2}}{2}$,y=$\sqrt{2}-1$时取“=”,故④错误;
⑤函数f(x)是定义在R上的周期为2的奇函数,当x∈[0,1]时,f(x)=x+1,则f($\frac{3}{2}$)=f($\frac{3}{2}-2$)=-f($\frac{1}{2}$)=-$\frac{3}{2}$,故⑤错误.
∴正确说法的个数是2个.
故选:B.
点评 本题考查命题的真假判断与应用,考查了命题的否定,考查函数的性质,训练了利用基本不等式求最值,是中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1] | C. | (1,+∞) | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | $\frac{4}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.384 | B. | 0.096 | C. | 0.616 | D. | 0.904 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
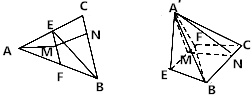 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com