
【题目】某家庭进行理财投资,根据长期收益率市场调查和预测,投资债券等稳键型产品A的收益与投资成正比,其关系如图1所示;投资股票等风险型产品B的收益与投资的算术平方根成正比,其关系如图2所示(收益与投资单位:万元). 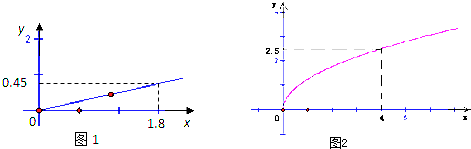
(1)分别将A、B两种产品的收益表示为投资的函数关系式;
(2)该家庭现有10万元资金,并全部投资债券等稳键型产品A及股票等风险型产品B两种产品,问:怎样分配这10万元投资,才能使投资获得最大收益,其最大收益为多少万元?
【答案】
(1)解:设投资为x万元,
A、B两产品获得的收益分别为f(x)、g(x)万元,
由题意,f(x)=k1x,g(x)= ![]() ,k1,k2≠0,x≥0,
,k1,k2≠0,x≥0,
又由图知f(1.8)=0.45,g(4)=2.5;解得 ![]() ,k2=
,k2= ![]() ,
,
∴f(x)= ![]() ,x≥0.g(x)=
,x≥0.g(x)= ![]()
(2)解:设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10﹣x)万元,
记家庭进行理财投资获取的收益为y万元,
则y= ![]() ,x≥0.
,x≥0.
设 ![]() ,则x=t2,0≤t≤
,则x=t2,0≤t≤ ![]() .
.
∴y=﹣ ![]() ,
,
当t= ![]() ,也即x=
,也即x= ![]() 时,y取最大值
时,y取最大值 ![]() .
.
答:对股票等风险型产品B投资 ![]() 万元,对债券等稳键型产品A投资
万元,对债券等稳键型产品A投资 ![]() 万元时,
万元时,
可获最大收益 ![]() 万元
万元
【解析】(1)设投资为x万元,A、B两产品获得的收益分别为f(x)、g(x)万元,由题意,f(x)=k1x,g(x)= ![]() ,k1 , k2≠0,x≥0,再由图象能求出A、B两种产品的收益表示为投资的函数关系式.(2)设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10﹣x)万元,记家庭进行理财投资获取的收益为y万元,则y=
,k1 , k2≠0,x≥0,再由图象能求出A、B两种产品的收益表示为投资的函数关系式.(2)设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10﹣x)万元,记家庭进行理财投资获取的收益为y万元,则y= ![]() ,x≥0.利用换元法能求出怎样分配这10万元投资,才能使投资获得最大收益,并能求出其最大收益为多少万元.
,x≥0.利用换元法能求出怎样分配这10万元投资,才能使投资获得最大收益,并能求出其最大收益为多少万元.


科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?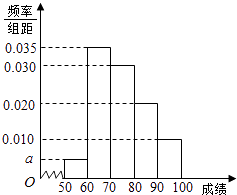
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是圆F1:(x﹣1)2+y2=8上任意一点,点F2与点F1关于原点对称,线段PF2的垂直平分线分别与PF1,PF2交于M,N两点.
(1)求点M的轨迹C的方程;
(2)过点G(0, ![]() )的动直线l与点的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
)的动直线l与点的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 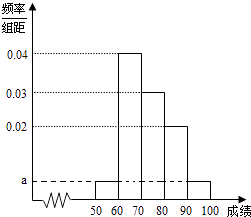
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C为锐角△ABC的内角, ![]() =(sinA,sinBsinC),
=(sinA,sinBsinC), ![]() =(1,﹣2),
=(1,﹣2), ![]() ⊥
⊥ ![]() .
.
(1)tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2)求tanAtanBtanC的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com