Question

18．三棱锥各顶点的坐标分别为（0，0，0），（1，0，0），（0，2，0），（0，0，3），则三棱锥的体积为1．

Answer 1

分析 由题意，C（0，0，0），A（1，0，0），B（0，2，0），P（0，0，3），则PC⊥平面ABC，CB⊥CA，利用两点间的距离可知AC，CB和PC，进而利用三棱锥体积公式求得答案．

解答 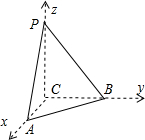解：由题意，C（0，0，0），A（1，0，0），B（0，2，0），P（0，0，3），则PC⊥平面ABC，CB⊥CA
则△ACB的面积=CA×CB÷2=1×2÷2=1，
则PC为三棱锥的高=3，
三棱锥的体积=△ACB的面积×高PC÷3=1×3÷3=1
故答案为：1．

点评 本题主要考查了点到面的距离计算和三棱锥的体积计算．点到平面的距离是立体几何的一个难点，其主要原因是垂线段难找，故垂线段是解题的关键．