
分析 (Ⅰ)直线C1的参数方程为$\left\{{\begin{array}{l}{x=1+t}\\{y=2+t}\end{array}}\right.(t$为参数),消去参数可得C1的普通方程.圆C2的方程为$ρ=-2cosθ+2\sqrt{3}sinθ$,即ρ2=-2ρcosθ+2$\sqrt{3}$ρsinθ,利用互化公式可得直角坐标方程.
(Ⅱ)利用点到直线的距离公式可得:圆心为$(-1,\sqrt{3})$到直线的距离d,利用|AB|=2$\sqrt{{2}^{2}-{d}^{2}}$即可得出.
解答 解:(Ⅰ)直线C1的参数方程为$\left\{{\begin{array}{l}{x=1+t}\\{y=2+t}\end{array}}\right.(t$为参数),
消去参数可得:C1的普通方程为x-y+1=0.
圆C2的方程为$ρ=-2cosθ+2\sqrt{3}sinθ$,
即ρ2=-2ρcosθ+2$\sqrt{3}$ρsinθ,
可得直角坐标方程:x2+y2+2x-2$\sqrt{3}$y=0,
配方可得:圆${C_2}:{(x+1)^2}+{(y-\sqrt{3})^2}=4$.
(Ⅱ)圆心为$(-1,\sqrt{3})$到直线的距离d=$\frac{|-1-\sqrt{3}+1|}{\sqrt{2}}$=$\frac{\sqrt{6}}{2}$,
∴|AB|=2$\sqrt{{2}^{2}-{d}^{2}}$=2$\sqrt{4-(\frac{\sqrt{6}}{2})^{2}}$=$\sqrt{10}$.
点评 本题考查了参数方程化为普通方程、极坐标与直角坐标方程互化、直线与圆相交弦长公式、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | -3 | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
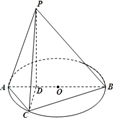 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=BD.
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{2}-1$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com