
| A. | 2 500 | B. | 2 600 | C. | 2 700 | D. | 2 80 |
分析 从左至右逐一列出逆序的个数再求和,即统计每个数后面的数中比它小的数的个数.由此能求出逆序数之和.
解答 解:从左至右逐一列出逆序的个数再求和,
即统计每个数后面的数中比它小的数的个数.
| 1 | 3 | 5 | 7 | 9 | … | 99 | 101 | 100 | 98 | 96 | … | 6 | 4 | 2 | |
| 逆序数 | 0 | 1 | 2 | 3 | 4 | … | 49 | 50 | 49 | 48 | 47 | … | 2 | 1 | 0 |
点评 本题考查排列的逆序数之和的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-∞,1) | C. | (-3,1) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {1} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
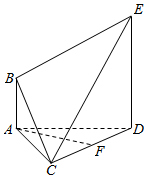 在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,$BC=\sqrt{5}$,F是CD的中点.
在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,$BC=\sqrt{5}$,F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
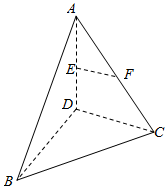 如图,四面体ABCD中,AD⊥平面BCD,E、F分别为AD、AC的中点,BC⊥CD.
如图,四面体ABCD中,AD⊥平面BCD,E、F分别为AD、AC的中点,BC⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com