
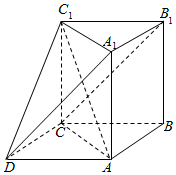
 如图所示的几何体中,ABC-A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.
如图所示的几何体中,ABC-A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.分析 (I)连接A1C交AC1于E,证明AA1⊥AC,CD⊥AC,推出CD⊥平面A1ACC1,然后证明AC1⊥平面A1 B1CD.
(II)如图建立直角坐标系,求出相关点的坐标,求出平面 AC1D的法向量$\overrightarrow{n_1}=({\sqrt{3},1,\frac{1}{λ}})$,平面C1CD的法向量为$\overrightarrow{n_2}=({0,1,0})$,通过向量的数量积求出λ=1,然后利用等体积法求解体积即可.
解答 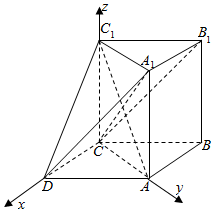 (I)证明:连接A1C交AC1于E,因为AA1=AC,又A A1⊥平面ABCD,所以AA1⊥AC,
(I)证明:连接A1C交AC1于E,因为AA1=AC,又A A1⊥平面ABCD,所以AA1⊥AC,
所以A1ACC1为正方形,所以A1C⊥AC1,…(2分)
在△ACD中,AD=2CD,∠ADC=60°,由余弦定理得 AC2=AD2+CD2-2 AC•DCcos60°,
所以${A}C=\sqrt{3}CD$,所以AD2=AC2+CD2,
所以CD⊥AC,又AA1⊥CD.所以CD⊥平面A1ACC1,
所以CD⊥AC1,所以AC1⊥平面A1 B1CD.…(6分)
(II)如图建立直角坐标系,则D(2,0,0),${A}({0,2\sqrt{3},0})$,${C_1}({0,0,2\sqrt{3}λ})$,${{A}_1}({0,2\sqrt{3},2\sqrt{3}λ})$∴$\overrightarrow{D{C_1}}=({-2,0,2\sqrt{3}λ})$,$\overrightarrow{D{{A}_1}}=({-2,2\sqrt{3},2\sqrt{3}λ})$
对平面 AC1D,因为$\overrightarrow{{A}D}=({2,-2\sqrt{3},0})$,$\overrightarrow{{A}{C_1}}=({0,-2\sqrt{3},2\sqrt{3}λ})$
所以法向量$\overrightarrow{n_1}=({\sqrt{3},1,\frac{1}{λ}})$,
平面C1CD的法向量为$\overrightarrow{n_2}=({0,1,0})$,…(8分)
由$cosθ=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}|•|{\overrightarrow{n_2}}|}}=\frac{1}{{\sqrt{3+1+{λ^{-2}}}}}=\frac{{\sqrt{5}}}{5}$,得λ=1,…(10分)
所以 A A1=AC,此时,CD=2,${A}{{A}_1}={A}C=2\sqrt{3}$,
所以${V_{{C_1}-{{A}_1}CD}}={V_{D-{{A}_1}C{C_1}}}=\frac{1}{3}×({\frac{1}{2}×2\sqrt{3}×2\sqrt{3}})×2=4$…(12分)
点评 本题考查二面角的平面镜的求法与应用,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | (0,1) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{13}}}{3}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{11}}}{33}$ | B. | $±\sqrt{3}$ | C. | $±\frac{{\sqrt{3}}}{3}$ | D. | $±3\sqrt{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com