
如图,在三棱锥 中,
中, ,
, ,
, 为
为 的中点,
的中点, ,
, =
= .
.

(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)见解析;(2) .
.
【解析】
试题分析:(1)欲证面面垂直,应先证线线垂直、线面垂直.注意到在 中的边长关系,应用勾股定理逆定理可得
中的边长关系,应用勾股定理逆定理可得 为直角三角形,
为直角三角形, .
.
又 ,且
,且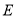 是
是 的中点,可得
的中点,可得 ,从而证得
,从而证得 平面
平面 ,即证得
,即证得
平面 平面
平面 .
.
(2)以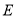 点为坐标原点,建立空间直角坐标系,利用“向量法”求解.
点为坐标原点,建立空间直角坐标系,利用“向量法”求解.
确定平面 的一个法向量为
的一个法向量为 ,
,
根据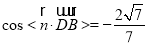 ,得到直线
,得到直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.
试题解析:(1)证明:在 中,
中, ,
,
 ,
,

 ,
,
则 为直角三角形,
为直角三角形,
所以, .
.
又由已知 ,
,
且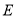 是
是 的中点,可得
的中点,可得
又 ,
,
 平面
平面
又 面
面
 平面
平面 平面
平面 .(6分)
.(6分)
(2)以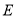 点为坐标原点,建立如图
点为坐标原点,建立如图
所示直角坐标系,
则
 ,
,
 .
.
设平面 的法向量为
的法向量为 ,则有
,则有
 即
即
解得: ,
,
所以,平面 的一个法向量为
的一个法向量为 ,
,
 ,
,
故直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .(12分)
.(12分)
考点:垂直关系,线面角的计算,空间向量的应用.


科目:高中数学 来源:2013-2014学年湖南省高三十三校联考第二次考试理科数学试卷(解析版) 题型:选择题
若实数a,b,c成等差数列,点 在动直线
在动直线 上的射影为
上的射影为 ,点
,点 ,则
,则 的最大值是( )
的最大值是( )
A. B.
B.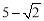 C.
C.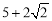 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省益阳市高三模拟考试理科数学试卷(解析版) 题型:选择题
下列有关命题的说法正确的是( )
A.命题“若 ,则
,则 ”的否命题为:“若
”的否命题为:“若 ,则
,则 ”.
”.
B.“ ” 是“
” 是“ ”的必要不充分条件.
”的必要不充分条件.
C.命题“若 ,则
,则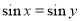 ”的逆否命题为真命题.
”的逆否命题为真命题.
D.命题“ R使得
R使得 ”的否定是:“
”的否定是:“ R均有
R均有 ”.
”.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省怀化市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
一只昆虫在边长分别为 、
、 、
、 的三角形区域内随机爬行,则其到三角形顶点的距离小于
的三角形区域内随机爬行,则其到三角形顶点的距离小于 的地方的概率为 .
的地方的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com