
【题目】已知函数f(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1.
(Ⅰ)求实数a,b的值;
(Ⅱ)设函数g(x)=![]() ,若不等式g(2x)﹣k2x≤0在x∈[﹣1,1]上恒成立,求实数k的取值范围.
,若不等式g(2x)﹣k2x≤0在x∈[﹣1,1]上恒成立,求实数k的取值范围.
【答案】(1)a=1,b=0;(2)![]()
【解析】
(Ⅰ)![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,可得
上单调递增,可得![]() ,解出即可;(Ⅱ)由(Ⅰ)可得
,解出即可;(Ⅱ)由(Ⅰ)可得![]() ,原题可化为
,原题可化为![]() ,分离参数
,分离参数![]() ,令
,令![]() ,求出
,求出![]() 的最大值即可.
的最大值即可.
解:(Ⅰ)f(x)=ax2﹣2ax+1+b=a(x﹣1)2+1+b﹣a.
∵a>0,∴f(x)在区间[2,3]上单调递增,
∴![]() ,解得a=1,b=0;
,解得a=1,b=0;
(Ⅱ)由(Ⅰ)知,f(x)=x2﹣2x+1,
∴g(x)=![]() =
=![]() ,
,
不等式g(2x)﹣k2x≤0可化为![]() ,
,
即k![]() .
.
令t=![]() ,
,
∵x∈[﹣1,1],∴t∈[![]() ,2],
,2],
令h(t)=t2﹣2t+1=(t﹣1)2,t∈[![]() ,2],
,2],
∴当t=2时,函数取得最大值h(2)=1.
∴k≥1.
∴实数k的取值范围为[1,+∞).


科目:高中数学 来源: 题型:
【题目】已知等差数列 ![]() 中,公差
中,公差 ![]() ,
, ![]() ,且
,且 ![]() 成等比数列.
成等比数列.
(1)求数列 ![]() 的通项公式;
的通项公式;
(2)若 ![]() 为数列
为数列 ![]() 的前
的前 ![]() 项和,且存在
项和,且存在 ![]() ,使得
,使得 ![]() 成立,求实数
成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 为
为![]() 上的奇函数,求实数a的值;
上的奇函数,求实数a的值;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 为减函数,求实数a的取值范围;
为减函数,求实数a的取值范围;
(3)是否存在实数![]() (
(![]() ),使得
),使得![]()
![]() 在闭区间
在闭区间![]() 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() 在
在![]() 上是单调递增函数,则
上是单调递增函数,则![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】∵![]() ,
,
∴![]() ,
,
又函数![]() 在
在![]() 单调递增,
单调递增,
∴![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立。
上恒成立。
又当![]() 时,
时, ![]() ,
,
∴![]() 。
。
又![]() ,
,
∴![]() 。
。
故实数![]() 的取值范围是
的取值范围是![]() 。
。
答案: ![]()
点睛:对于导函数和函数单调性的关系要分清以下结论:
(1)当![]() 时,若
时,若![]() ,则
,则![]() 在区间D上单调递增(减);
在区间D上单调递增(减);
(2)若函数![]() 在区间D上单调递增(减),则
在区间D上单调递增(减),则![]() 在区间D上恒成立。即解题时可将函数单调性的问题转化为
在区间D上恒成立。即解题时可将函数单调性的问题转化为![]() 的问题,但此时不要忘记等号。
的问题,但此时不要忘记等号。
【题型】填空题
【结束】
19
【题目】某珠宝店丢了一件珍贵珠宝,以下四人中只有一人说真话,只有一人偷了珠宝.甲:我没有偷;乙:丙是小偷;丙:丁是小偷;丁:我没有偷.根据以上条件,可以判断偷珠宝的人是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,离心率
,离心率![]() ,短轴长为2.
,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 为椭圆上的一动点(非长轴端点),
为椭圆上的一动点(非长轴端点),![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,若
点,若![]() 面积为
面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]()
【解析】试题分析:(Ⅰ)由题意得![]() ,再由
,再由![]()
![]() 椭圆的方程为
椭圆的方程为![]() ;(Ⅱ)①当直线
;(Ⅱ)①当直线![]() 斜率不存在时,不妨取
斜率不存在时,不妨取![]() 面积为
面积为![]()
![]() ,不符合题意. ②当直线
,不符合题意. ②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() , 由
, 由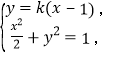
![]() 得
得![]()
![]()
![]()
![]() ,再求点
,再求点![]() 的直线
的直线![]() 的距离
的距离![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]() 面积为
面积为![]()
![]()
![]()
![]() ∴
∴![]() 或
或![]()
![]() 所求方程为
所求方程为![]() 或
或![]() .
.
试题解析: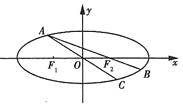
(Ⅰ)由题意得![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴椭圆的方程为![]() .
.
(Ⅱ)①当直线![]() 斜率不存在时,不妨取
斜率不存在时,不妨取![]() ,
,
∴![]() 面积为
面积为![]()
![]() ,不符合题意.
,不符合题意.
②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,
,
由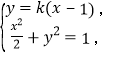 化简得
化简得![]() ,
,
设![]() ,
,
∴![]()
![]() ,
,
∵点![]() 的直线
的直线![]() 的距离
的距离![]() ,
,
又![]() 是线段
是线段![]() 的中点,∴点
的中点,∴点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴![]() 面积为
面积为![]()
![]()
![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() ,
,
∴直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【题型】解答题
【结束】
25
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)若![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. (Ⅰ)求证:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为2的正三角形ABC沿x轴滚动,记滚动过程中顶点A的横、纵坐标分别为![]() 和
和![]() ,且
,且![]() 是
是![]() 在映射
在映射![]() 作用下的象,则下列说法中:
作用下的象,则下列说法中:

① 映射![]() 的值域是
的值域是![]() ;
;
② 映射![]() 不是一个函数;
不是一个函数;
③ 映射![]() 是函数,且是偶函数;
是函数,且是偶函数;
④ 映射![]() 是函数,且单增区间为
是函数,且单增区间为![]() ,
,
其中正确说法的序号是___________.
说明:“正三角形ABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点B为中心顺时针旋转,当顶点C落在x轴上时,再以顶点C为中心顺时针旋转,如此继续.类似地,正三角形ABC可以沿x轴负方向滚动.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当|a|≤1,|x|≤1时,关于x的不等式|x2﹣ax﹣a2|≤m恒成立,则实数m的取值范围是( )
A.[ ![]() ,+∞)
,+∞)
B.[ ![]() ,+∞)
,+∞)
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com