
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФзѓЁЂгвСНИіНЙЕуЗжБ№ЮЊ
ЕФзѓЁЂгвСНИіНЙЕуЗжБ№ЮЊ![]() ЃЌРыаФТЪ
ЃЌРыаФТЪ![]() ЃЌЖЬжсГЄЮЊ2.
ЃЌЖЬжсГЄЮЊ2.
ЃЈЂёЃЉЧѓЭждВЕФЗНГЬЃЛ
ЃЈЂђЃЉЩшЕу![]() ЮЊЭждВЩЯЕФвЛЖЏЕуЃЈЗЧГЄжсЖЫЕуЃЉЃЌ
ЮЊЭждВЩЯЕФвЛЖЏЕуЃЈЗЧГЄжсЖЫЕуЃЉЃЌ![]() ЕФбгГЄЯпгыЭждВНЛгк
ЕФбгГЄЯпгыЭждВНЛгк![]() ЕуЃЌ
ЕуЃЌ![]() ЕФбгГЄЯпгыЭждВНЛгк
ЕФбгГЄЯпгыЭждВНЛгк![]() ЕуЃЌШє
ЕуЃЌШє![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЈЂђЃЉ
ЃЈЂђЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈЂёЃЉгЩЬтвтЕУ![]() ЃЌдйгЩ
ЃЌдйгЩ![]()
![]() ЭждВЕФЗНГЬЮЊ
ЭждВЕФЗНГЬЮЊ![]() ЃЛЃЈЂђЃЉЂйЕБжБЯп
ЃЛЃЈЂђЃЉЂйЕБжБЯп![]() аБТЪВЛДцдкЪБЃЌВЛЗСШЁ
аБТЪВЛДцдкЪБЃЌВЛЗСШЁ![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]() ЃЌВЛЗћКЯЬтвт. ЂкЕБжБЯп
ЃЌВЛЗћКЯЬтвт. ЂкЕБжБЯп![]() аБТЪДцдкЪБЃЌЩшжБЯп
аБТЪДцдкЪБЃЌЩшжБЯп![]() ЃЌ гЩ
ЃЌ гЩ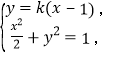
![]() ЕУ
ЕУ![]()
![]()
![]()
![]() ЃЌдйЧѓЕу
ЃЌдйЧѓЕу![]() ЕФжБЯп
ЕФжБЯп![]() ЕФОрРы
ЕФОрРы![]()
![]() Еу
Еу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]()
![]()
![]() Ёр
Ёр![]() Лђ
Лђ![]()
![]() ЫљЧѓЗНГЬЮЊ
ЫљЧѓЗНГЬЮЊ![]() Лђ
Лђ![]() .
.
ЪдЬтНтЮіЃК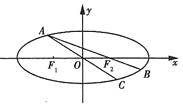
ЃЈЂёЃЉгЩЬтвтЕУ![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁрЭждВЕФЗНГЬЮЊ![]() .
.
ЃЈЂђЃЉЂйЕБжБЯп![]() аБТЪВЛДцдкЪБЃЌВЛЗСШЁ
аБТЪВЛДцдкЪБЃЌВЛЗСШЁ![]() ЃЌ
ЃЌ
Ёр![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]() ЃЌВЛЗћКЯЬтвт.
ЃЌВЛЗћКЯЬтвт.
ЂкЕБжБЯп![]() аБТЪДцдкЪБЃЌЩшжБЯп
аБТЪДцдкЪБЃЌЩшжБЯп![]() ЃЌ
ЃЌ
гЩ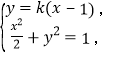 ЛЏМђЕУ
ЛЏМђЕУ![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ
ЁпЕу![]() ЕФжБЯп
ЕФжБЯп![]() ЕФОрРы
ЕФОрРы![]() ЃЌ
ЃЌ
гж![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌЁрЕу
ЕФжаЕуЃЌЁрЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌ
ЃЌ
Ёр![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]()
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЁржБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() Лђ
Лђ![]() .
.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфгыМЋжЕЃЛ
ЕФЕЅЕїЧјМфгыМЋжЕЃЛ
ЃЈЂђЃЉШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌжЄУїЃК
ЃЌжЄУїЃК ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЕФЕЅЕїдіЧјМфЮЊ
ЕФЕЅЕїдіЧјМфЮЊ![]() ЃЌЕЅЕїМѕЧјМфЮЊ
ЃЌЕЅЕїМѕЧјМфЮЊ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() дк
дк![]() ДІШЁЕУМЋДѓжЕ
ДІШЁЕУМЋДѓжЕ![]() ЃЌЧв
ЃЌЧв![]() ЃЛЃЈ2ЃЉМћНтЮі.
ЃЛЃЈ2ЃЉМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓЕМЪ§ЃЌдйЧѓЕМКЏЪ§СуЕуЃЌСаБэЗжЮіЕМКЏЪ§ЗћКХБфЛЏЙцТЩЃЌНјЖјШЗЖЈЕЅЕїЧјМфвдМАМЋжЕЃЈ2ЃЉЮЊМЋжЕЕуЦЋвЦЮЪЬтЃЌЯШЙЙдьКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌИљОнЕМЪ§ПЩЕУ
ЃЌИљОнЕМЪ§ПЩЕУ![]() ЕЅЕїадЃЌМДЕУ
ЕЅЕїадЃЌМДЕУ![]() ЃЌзюКѓИљОн
ЃЌзюКѓИљОн![]() ЕЅЕїадЕУ
ЕЅЕїадЕУ![]() ЃЌМДжЄЕУНсТл
ЃЌМДжЄЕУНсТл
ЪдЬтНтЮіЃКЃЈЂёЃЉгЩ![]() ЃЌ
ЃЌ
взЕУ![]() ЕФЕЅЕїдіЧјМфЮЊ
ЕФЕЅЕїдіЧјМфЮЊ![]() ЃЌЕЅЕїМѕЧјМфЮЊ
ЃЌЕЅЕїМѕЧјМфЮЊ![]() ЃЌ
ЃЌ
КЏЪ§![]() дк
дк![]() ДІШЁЕУМЋДѓжЕ
ДІШЁЕУМЋДѓжЕ![]() ЃЌЧв
ЃЌЧв![]()
ЃЈЂђЃЉгЩ![]() ЃЌ
ЃЌ ![]() ЃЌВЛЗСЩш
ЃЌВЛЗСЩш![]() ЃЌдђБига
ЃЌдђБига![]() ЃЌ
ЃЌ
ЙЙдьКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
дђ![]()
![]() ЃЌЫљвд
ЃЌЫљвд![]() дк
дк![]() ЩЯЕЅЕїЕндіЃЌ
ЩЯЕЅЕїЕндіЃЌ ![]() ЃЌвВМД
ЃЌвВМД![]() Жд
Жд![]() КуГЩСЂ.
КуГЩСЂ.
гЩ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ыљвд![]()
![]()
![]() ЃЌ
ЃЌ
МД![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌЧв
ЃЌЧв![]() дк
дк![]() ЩЯЕЅЕїЕнМѕЃЌ
ЩЯЕЅЕїЕнМѕЃЌ
Ыљвд![]() ЃЌМДжЄ
ЃЌМДжЄ![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§ ![]() ЃЌАбКЏЪ§
ЃЌАбКЏЪ§ ![]() ЕФЭМЯѓЯђгвЦНвЦ
ЕФЭМЯѓЯђгвЦНвЦ ![]() ИіЕЅЮЛЃЌЕУЕНКЏЪ§
ИіЕЅЮЛЃЌЕУЕНКЏЪ§ ![]() ЕФЭМЯѓЃЌШє
ЕФЭМЯѓЃЌШє ![]() ЪЧ
ЪЧ ![]() дк
дк ![]() ФкЕФСНИљЃЌдђ
ФкЕФСНИљЃЌдђ ![]() ЕФжЕЮЊЃЈ ЃЉ
ЕФжЕЮЊЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌШєЭЌЪБТњзувдЯТЬѕМўЃК
ЃЌШєЭЌЪБТњзувдЯТЬѕМўЃК
Ђй![]() дкDЩЯЕЅЕїЕнМѕЛђЕЅЕїЕндіЃЛ
дкDЩЯЕЅЕїЕнМѕЛђЕЅЕїЕндіЃЛ
ЂкДцдкЧјМф![]() ЃЌЪЙ
ЃЌЪЙ![]() дк
дк![]() ЩЯЕФжЕгђЪЧ
ЩЯЕФжЕгђЪЧ![]() ЃЌФЧУДГЦ
ЃЌФЧУДГЦ![]() ЮЊБеКЏЪ§ЃЎ
ЮЊБеКЏЪ§ЃЎ
ЃЈ1ЃЉЧѓБеКЏЪ§![]() ЗћКЯЬѕМўЂкЕФЧјМф
ЗћКЯЬѕМўЂкЕФЧјМф![]() ЃЛ
ЃЛ
ЃЈ2ЃЉХаЖЯКЏЪ§![]() ЪЧВЛЪЧБеКЏЪ§ЃПШєЪЧЧыевГіЧјМф
ЪЧВЛЪЧБеКЏЪ§ЃПШєЪЧЧыевГіЧјМф![]() ЃЛШєВЛЪЧЧыЫЕУїРэгЩЃЛ
ЃЛШєВЛЪЧЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШє![]() ЪЧБеКЏЪ§ЃЌЧѓЪЕЪ§
ЪЧБеКЏЪ§ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§f(x)ЃНlnxЃЋ2xЃ6ЁЃ
(1)жЄУїЃККЏЪ§f(x)дкЦфЖЈвхгђЩЯЪЧдіКЏЪ§ЃЛ
(2)жЄУїЃККЏЪ§f(x)гаЧвжЛгавЛИіСуЕуЃЛ
(3)ЧѓетИіСуЕуЫљдкЕФвЛИіЧјМфЃЌЪЙетИіЧјМфЕФГЄЖШВЛГЌЙ§![]() ЁЃ
ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГздааГЕГЇЮЊЙВЯэЕЅГЕЙЋЫОЩњВњаТбљЪНЕФЕЅГЕЃЌвбжЊЩњВњаТбљЪНЕЅГЕЕФЙЬЖЈГЩБОЮЊ20000дЊЃЌУПЩњВњвЛМўаТбљЪНЕЅГЕашвЊдіМгЭЖШы100дЊЃЎИљОнГѕВНВтЫуЃЌздааГЕГЇЕФзмЪевцЃЈЕЅЮЛЃКдЊЃЉТњзуЗжЖЮКЏЪ§hЃЈxЃЉЃЌЦфжа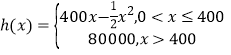 ,xЪЧаТбљЪНЕЅГЕЕФдТВњСПЃЈЕЅЮЛЃКМўЃЉЃЌРћШѓ=змЪевцЉзмГЩБОЃЎ
,xЪЧаТбљЪНЕЅГЕЕФдТВњСПЃЈЕЅЮЛЃКМўЃЉЃЌРћШѓ=змЪевцЉзмГЩБОЃЎ
ЃЈ1ЃЉЪдНЋздааГЕГЇЕФРћШѓyдЊБэЪОЮЊдТВњСПxЕФКЏЪ§ЃЛ
ЃЈ2ЃЉЕБдТВњСПЮЊЖрЩйМўЪБздааГЕГЇЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=ax2Љ2ax+1+bЃЈaЃО0ЃЉдкЧјМф[2ЃЌ3]ЩЯгазюДѓжЕ4КЭзюаЁжЕ1ЃЎ
ЃЈЂёЃЉЧѓЪЕЪ§aЃЌbЕФжЕЃЛ
ЃЈЂђЃЉЩшКЏЪ§gЃЈxЃЉ=![]() ЃЌШєВЛЕШЪНgЃЈ2xЃЉЉk2xЁм0дкxЁЪ[Љ1ЃЌ1]ЩЯКуГЩСЂЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
ЃЌШєВЛЕШЪНgЃЈ2xЃЉЉk2xЁм0дкxЁЪ[Љ1ЃЌ1]ЩЯКуГЩСЂЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=logaЃЈ1+xЃЉЃЌgЃЈxЃЉ=logaЃЈ1ЉxЃЉЃЌЃЈaЃО1ЃЉЃЎ
ЃЈ1ЃЉЧѓКЏЪ§h(x)=fЃЈxЃЉЉgЃЈxЃЉЕФЖЈвхгђЃЛ
ЃЈ2ЃЉЧѓЪЙfЃЈxЃЉЉgЃЈxЃЉЃО0ЕФxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкКЏЪ§fЃЈxЃЉ= ![]() ЃЌЩшf2ЃЈxЃЉ=f[fЃЈxЃЉ]ЃЌf3ЃЈxЃЉ=f[f2ЃЈxЃЉ]ЃЌЁЃЌfn+1ЃЈxЃЉ=f[fnЃЈxЃЉ]ЃЈnЁЪN* ЃЌ ЧвnЁн2ЃЉЃЌСюМЏКЯM={x|f2036ЃЈxЃЉ=xЃЌxЁЪR}ЃЌдђМЏКЯMЮЊЃЈ ЃЉ
ЃЌЩшf2ЃЈxЃЉ=f[fЃЈxЃЉ]ЃЌf3ЃЈxЃЉ=f[f2ЃЈxЃЉ]ЃЌЁЃЌfn+1ЃЈxЃЉ=f[fnЃЈxЃЉ]ЃЈnЁЪN* ЃЌ ЧвnЁн2ЃЉЃЌСюМЏКЯM={x|f2036ЃЈxЃЉ=xЃЌxЁЪR}ЃЌдђМЏКЯMЮЊЃЈ ЃЉ
A.ПеМЏ
B.ЪЕЪ§МЏ
C.ЕЅдЊЫиМЏ
D.ЖўдЊЫиМЏ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋШ§ПХїЛзгИїжРвЛДЮЃЌМЧЪТМўA=ЁАШ§ИіЕуЪ§ЖМВЛЭЌЁБЃЌB=ЁАжСЩйГіЯжвЛИі6ЕуЁБЃЌдђЬѕМўИХТЪPЃЈA|BЃЉЃЌPЃЈB|AЃЉЗжБ№ЪЧЃЈ ЃЉ
A.![]() ЃЌ
ЃЌ ![]()
B.![]() ЃЌ
ЃЌ ![]()
C.![]() ЃЌ
ЃЌ ![]()
D.![]() ЃЌ
ЃЌ ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com