
����Ŀ��ij���г���Ϊ����������˾��������ʽ�ĵ�������֪��������ʽ�����Ĺ̶��ɱ�Ϊ20000Ԫ��ÿ����һ������ʽ������Ҫ����Ͷ��100Ԫ�����ݳ������㣬���г����������棨��λ��Ԫ������ֶκ���h��x��������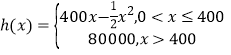 ,x������ʽ�������²�������λ������������=�����橁�ܳɱ���
,x������ʽ�������²�������λ������������=�����橁�ܳɱ���
��1���Խ����г���������yԪ��ʾΪ�²���x�ĺ�����
��2�����²���Ϊ���ټ�ʱ���г��������������������Ƕ��٣�
���𰸡���1����������2�����²���x=300��ʱ�����г�������������������Ϊ25000Ԫ
��������
��1������ܳɱ���������=������-�ܳɱ��ɵ����г���������![]() Ԫ���²���
Ԫ���²���![]() �ĺ���ʽ����2����
�ĺ���ʽ����2����![]() ʱ�������䷽������κ��������ֵ25000����
ʱ�������䷽������κ��������ֵ25000����![]() ʱ���ɺ����ĵ����Կɵ�
ʱ���ɺ����ĵ����Կɵ�![]() ���ɴ˵ô𰸣�
���ɴ˵ô𰸣�
�⣺��1�������裬�ܳɱ�Ϊ20000+100x��
��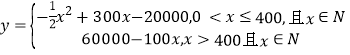 ��
��
��2����0��x��400ʱ��![]() ��
��
��x=300ʱ��ymax=25000��
��x��400ʱ��y=60000��100x�Ǽ�������
��y��60000��100��400=20000��
�൱�²���x=300��ʱ�����г�������������������Ϊ25000Ԫ��


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ���ҽ�����������
���ҽ�����������![]() �Ľ����غϣ��Ҹ���Բ����������˫����
�Ľ����غϣ��Ҹ���Բ����������˫����![]() �������ʻ�Ϊ����.
�������ʻ�Ϊ����.
��1������Բ�ķ��̣�
��2����ֱ��![]() ����Բ�ཻ�ڲ�ͬ������
����Բ�ཻ�ڲ�ͬ������![]() ����֪��
����֪��![]() ������Ϊ
������Ϊ![]() ����
����![]() ���߶�
���߶�![]() �Ĵ�ֱƽ�����ϣ���
�Ĵ�ֱƽ�����ϣ���![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�D��AC���е㣬A1D��ƽ��ABC��AB=BC��ƽ��BB1D����A1C1���ڵ�E��
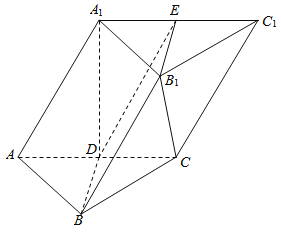
��1����֤��AC��A1B��
��2����֤��ƽ��BB1D��ƽ��AA1C1C��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�Ϊ��ǡ�ABC�����ڽ�A��B��C�ĶԱߣ��ң�a+b����sinA��sinB��=��c��b��sinC �������A�Ĵ�С��
������f��x��= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]() ����f��B����ȡֵ��Χ��
����f��B����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB��CD��AD=DC=CB=1����BCD=120�㣬�ı���BFED����BDΪֱ������ֱ�����Σ�DE=2BF=2��ƽ��BFED��ƽ��ABCD�� ������֤��AD��ƽ��BFED��
�������߶�EF���Ƿ����һ��P��ʹ��ƽ��PAB��ƽ��ADE���ɵ������ǵ�����ֵΪ ![]() �������ڣ������P��λ�ã��������ڣ�˵�����ɣ�
�������ڣ������P��λ�ã��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������������ֱ�Ϊ
��������������ֱ�Ϊ![]() ��������
��������![]() �����᳤Ϊ2.
�����᳤Ϊ2.
��������Բ�ķ��̣�
�������![]() Ϊ��Բ�ϵ�һ���㣨�dz���˵㣩��
Ϊ��Բ�ϵ�һ���㣨�dz���˵㣩��![]() ���ӳ�������Բ����
���ӳ�������Բ����![]() �㣬
�㣬![]() ���ӳ�������Բ����
���ӳ�������Բ����![]() �㣬��
�㣬��![]() ���Ϊ
���Ϊ![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
���𰸡�����![]() ����
����![]() ��
��![]()
����������������������������![]() ������
������![]()
![]() ��Բ�ķ���Ϊ
��Բ�ķ���Ϊ![]() �����ٵ�ֱ��
�����ٵ�ֱ��![]() б�ʲ�����ʱ������ȡ
б�ʲ�����ʱ������ȡ![]() ���Ϊ
���Ϊ![]()
![]() ������������. �ڵ�ֱ��
������������. �ڵ�ֱ��![]() б�ʴ���ʱ����ֱ��
б�ʴ���ʱ����ֱ��![]() �� ��
�� ��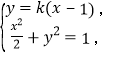
![]() ��
��![]()
![]()
![]()
![]() �������
�������![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]()
![]() ��
��![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ���Ϊ
���Ϊ![]()
![]()
![]()
![]() ��
��![]() ��
��![]()
![]() ����Ϊ
����Ϊ![]() ��
��![]() .
.
���������
�����������![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
����Բ�ķ���Ϊ![]() .
.
���ٵ�ֱ��![]() б�ʲ�����ʱ������ȡ
б�ʲ�����ʱ������ȡ![]() ��
��
��![]() ���Ϊ
���Ϊ![]()
![]() ������������.
������������.
�ڵ�ֱ��![]() б�ʴ���ʱ����ֱ��
б�ʴ���ʱ����ֱ��![]() ��
��
��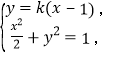 �����
�����![]() ��
��
��![]() ��
��
��![]()
![]() ��
��
�ߵ�![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ��
��
��![]() ���߶�
���߶�![]() ���е㣬���
���е㣬���![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ��
��
��![]() ���Ϊ
���Ϊ![]()
![]()
![]() ��
��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ��
��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��![]() .
.
�����͡������
��������
25
����Ŀ����֪����![]() .
.
��������![]() �ĵ��������뼫ֵ��
�ĵ��������뼫ֵ��
������![]() ����
����![]() ��֤����
��֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ���a��b��c���㣨a��b����4xcosB��ycosC=ccosB�ϣ�
��1��cosB��ֵ��
��2���� ![]()
![]() =3��b=3
=3��b=3 ![]() ����a��c��
����a��c��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��Ϊ��ǣ���cosA��sinB�ǡ�ABCΪ�۽������εģ� ��
A.��ֲ���Ҫ����
B.��Ҫ���������
C.��Ҫ����
D.�Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() �����䳤�᳤Ϊ__________����
�����䳤�᳤Ϊ__________����![]() Ϊ
Ϊ![]() ���ҽ��㣬
���ҽ��㣬 ![]() Ϊ
Ϊ![]() ���϶��㣬
���϶��㣬 ![]() Ϊ
Ϊ![]() ��λ�ڵ�һ�����ڵĶ��㣬���ı���
��λ�ڵ�һ�����ڵĶ��㣬���ı���![]() ����������ֵΪ__________��
����������ֵΪ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com