
【题目】已知函数![]() ,若同时满足以下条件:
,若同时满足以下条件:
①![]() 在D上单调递减或单调递增;
在D上单调递减或单调递增;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么称
,那么称![]() 为闭函数.
为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是不是闭函数?若是请找出区间
是不是闭函数?若是请找出区间![]() ;若不是请说明理由;
;若不是请说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)由![]() 在R上单减,列出方程组,即可求
在R上单减,列出方程组,即可求![]() 的值;
的值;
(2)由函数y=2x+lgx在(0,+∞)单调递增可知![]() 即
即![]() ,结合对数函数的单调性可判断
,结合对数函数的单调性可判断
(3)易知![]() 在[﹣2,+∞)上单调递增.设满足条件B的区间为[a,b],则方程组
在[﹣2,+∞)上单调递增.设满足条件B的区间为[a,b],则方程组![]() 有解,方程
有解,方程![]() 至少有两个不同的解,即方程x2﹣(2k+1)x+k2﹣2=0有两个都不小于k的不根.结合二次方程的实根分布可求k的范围
至少有两个不同的解,即方程x2﹣(2k+1)x+k2﹣2=0有两个都不小于k的不根.结合二次方程的实根分布可求k的范围
解:(1)∵![]() 在R上单减,所以区间[a,b]满足
在R上单减,所以区间[a,b]满足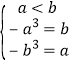 ,
,
解得a=﹣1,b=1
(2)∵函数y=2x+lgx在(0,+∞)单调递增
假设存在满足条件的区间[a,b],a<b,则![]() ,即
,即![]()
∴lgx=﹣x在(0,+∞)有两个不同的实数根,但是结合对数函数的单调性可知,y=lgx与y=﹣x只有一个交点
故不存在满足条件的区间[a,b],函数y=2x+lgx是不是闭函数
(3)易知![]() 在[﹣2,+∞)上单调递增.
在[﹣2,+∞)上单调递增.
设满足条件B的区间为[a,b],则方程组![]() 有解,方程
有解,方程![]() 至少有两个不同的解
至少有两个不同的解
即方程x2﹣(2k+1)x+k2﹣2=0有两个都不小于k的不根.
∴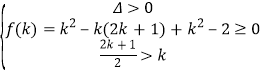 得
得![]() ,即所求.
,即所求.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F(1,0),且点(﹣1,
的右焦点为F(1,0),且点(﹣1, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点Q,使得 ![]() 恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知互不重合的直线![]() ,互不重合的平面
,互不重合的平面![]() ,给出下列四个命题,正确命题的个数是
,给出下列四个命题,正确命题的个数是
①若![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,则
,则![]()
![]()
![]()
②若![]() ,
,![]() ,
,![]() 则
则![]()
③若![]() ,
,![]() ,
,![]() ,则
,则![]()
④若![]()
![]()
![]() ,
,![]()
![]()
![]() ,则
,则![]() //
//![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D是AC的中点,A1D⊥平面ABC,AB=BC,平面BB1D与棱A1C1交于点E.
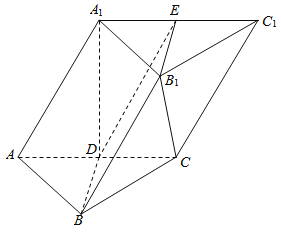
(1)求证:AC⊥A1B;
(2)求证:平面BB1D⊥平面AA1C1C;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 为
为![]() 上的奇函数,求实数a的值;
上的奇函数,求实数a的值;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 为减函数,求实数a的取值范围;
为减函数,求实数a的取值范围;
(3)是否存在实数![]() (
(![]() ),使得
),使得![]()
![]() 在闭区间
在闭区间![]() 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,且(a+b)(sinA﹣sinB)=(c﹣b)sinC (Ⅰ)求∠A的大小;
(Ⅱ)若f(x)= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]() ,求f(B)的取值范围.
,求f(B)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,离心率
,离心率![]() ,短轴长为2.
,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 为椭圆上的一动点(非长轴端点),
为椭圆上的一动点(非长轴端点),![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,若
点,若![]() 面积为
面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]()
【解析】试题分析:(Ⅰ)由题意得![]() ,再由
,再由![]()
![]() 椭圆的方程为
椭圆的方程为![]() ;(Ⅱ)①当直线
;(Ⅱ)①当直线![]() 斜率不存在时,不妨取
斜率不存在时,不妨取![]() 面积为
面积为![]()
![]() ,不符合题意. ②当直线
,不符合题意. ②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() , 由
, 由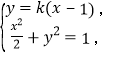
![]() 得
得![]()
![]()
![]()
![]() ,再求点
,再求点![]() 的直线
的直线![]() 的距离
的距离![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]() 面积为
面积为![]()
![]()
![]()
![]() ∴
∴![]() 或
或![]()
![]() 所求方程为
所求方程为![]() 或
或![]() .
.
试题解析: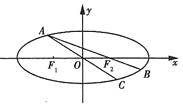
(Ⅰ)由题意得![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴椭圆的方程为![]() .
.
(Ⅱ)①当直线![]() 斜率不存在时,不妨取
斜率不存在时,不妨取![]() ,
,
∴![]() 面积为
面积为![]()
![]() ,不符合题意.
,不符合题意.
②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,
,
由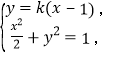 化简得
化简得![]() ,
,
设![]() ,
,
∴![]()
![]() ,
,
∵点![]() 的直线
的直线![]() 的距离
的距离![]() ,
,
又![]() 是线段
是线段![]() 的中点,∴点
的中点,∴点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴![]() 面积为
面积为![]()
![]()
![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() ,
,
∴直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【题型】解答题
【结束】
25
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)若![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com