
【题目】为了了解甲、乙两名同学的数学学习情况,对他们的![]() 次数学测试成绩(满分
次数学测试成绩(满分![]() 分)进行统计,作出如下的茎叶图,其中
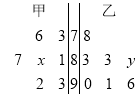
分)进行统计,作出如下的茎叶图,其中![]() 处的数字模糊不清,已知甲同学成绩的中位数是
处的数字模糊不清,已知甲同学成绩的中位数是![]() ,乙同学成绩的平均分是
,乙同学成绩的平均分是![]() 分.
分.
(1)求![]() 和
和![]() 的值;
的值;
(2)现从成绩在![]() 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据中位线定义可得![]() ,再根据平均数定义得
,再根据平均数定义得![]() (2)成绩在
(2)成绩在![]() 之间的试卷共有5份,利用枚举法可得随机抽取两份共有10种不同取法,而其中恰抽到一份甲同学试卷的基本事件数为6种,因此所求概率为
之间的试卷共有5份,利用枚举法可得随机抽取两份共有10种不同取法,而其中恰抽到一份甲同学试卷的基本事件数为6种,因此所求概率为![]()
试题解析:(1)![]() 甲同学成绩的中位数是
甲同学成绩的中位数是![]() ,
,![]() ,
,![]() 乙同学的平均分是
乙同学的平均分是![]() 分,
分,![]() .
.
(2)甲同学成绩在![]() 之间的试卷有二份,分别记为
之间的试卷有二份,分别记为![]() ,
,
乙同学成绩在![]() 之间的试卷有三份,分别记为
之间的试卷有三份,分别记为![]() ,
,
“从这五份试卷中随机抽取两份试卷”的所有可能结果为:
![]() ,
,![]() 共有
共有![]() 种情况,
种情况,
记“从成绩在![]() 之间的试卷随机抽取两份,恰抽到一份甲同学试卷”为事件
之间的试卷随机抽取两份,恰抽到一份甲同学试卷”为事件![]() ,则事件
,则事件![]() 包
包
含的基本事件为:![]() 共有
共有![]() 种情况,则
种情况,则![]() ,
,
故从成绩在![]() 之间的试卷中随机抽取两份进行分析,恰抽到一份甲同学试卷的概率为
之间的试卷中随机抽取两份进行分析,恰抽到一份甲同学试卷的概率为![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】为了参加市高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出![]() 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
人数 | 12 | 6 | 9 | 9 |
(1)现采取分层抽样的方法从这四个班中抽取运动员,求应分别从这四个班抽出的队员人数;
(2)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() :
:![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且到原点的距离为
上,且到原点的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项的和.
项的和.
(1)若数列![]() 为等差数列.
为等差数列.
①求数列的通项![]() ;
;
②若数列![]() 满足
满足![]() ,数列
,数列![]() 满足
满足![]() ,试比较数列
,试比较数列![]() 前
前![]() 项和
项和![]() 与
与![]() 前
前![]() 项和
项和![]() 的大小;
的大小;
(2)若对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点与两焦点构成的三角形为正三角形.
,上顶点与两焦点构成的三角形为正三角形.
(1)求椭圆![]() 的离心率;
的离心率;
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 的内切圆的面积的最大值为
的内切圆的面积的最大值为![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com