
 如图,在平面直角坐标系xoy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过点M的直线与抛物线交于A,B两点,设A(x1,y1)到准线l的距离d=2λp(λ>0)
如图,在平面直角坐标系xoy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过点M的直线与抛物线交于A,B两点,设A(x1,y1)到准线l的距离d=2λp(λ>0)分析 (1)求得抛物线的焦点和准线方程,由题意可得AF⊥x轴,即有p=3,进而得到抛物线的方程;
(2)设B(x2,y2),AB:y=k(x+$\frac{p}{2}$),代入抛物线的方程,可得x的方程,运用判别式大于0和求根公式,运用向量共线的坐标表示,可得2p=x2-x1,解方程即可得到所求定值.
解答 解:(1)抛物线y2=2px的焦点F($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$,
则|AF|=y1,可得AF⊥x轴,
则x1=$\frac{p}{2}$,即有d=$\frac{p}{2}$+$\frac{p}{2}$=3,即p=3,
则抛物线的方程为y2=6x;
(2)证明:设B(x2,y2),AB:y=k(x+$\frac{p}{2}$),代入抛物线的方程,可得
k2x2+p(k2-2)x+$\frac{{k}^{2}{p}^{2}}{4}$=0,
由△=p2(k2-2)2-k4p2>0,即为k2<1,
x1=$\frac{-p({k}^{2}-2)-2p\sqrt{1-{k}^{2}}}{2{k}^{2}}$,x2=$\frac{-p({k}^{2}-2)+2p\sqrt{1-{k}^{2}}}{2{k}^{2}}$,
由d=2λp,可得x1+$\frac{p}{2}$=2λp,
由$\overrightarrow{AM}$+λ$\overrightarrow{AB}$=$\overrightarrow{0}$,M(-$\frac{p}{2}$,0),
可得x1+$\frac{p}{2}$=λ(x2-x1),
即有2p=x2-x1=$\frac{2p\sqrt{1-{k}^{2}}}{{k}^{2}}$,
解得k2=$\frac{\sqrt{5}-1}{2}$.
故直线AB的斜率的平方为定值.
点评 本题考查抛物线的定义、方程和性质,注意定义法的运用,考查直线方程和抛物线的方程联立,求交点,考查向量共线的坐标表示,以及化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知电流I与时间t的关系式为I=Asin(ωt+φ).
已知电流I与时间t的关系式为I=Asin(ωt+φ).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
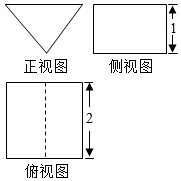 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 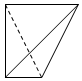 | C. | 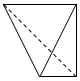 | D. | 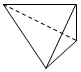 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com