
����Ŀ��Ϊ����Ӧ���Һ��٣�ijУ��֯����ѧ�����������������࣬������������֪ʶ�ʾ����𣬲���ѧ������������Ϊ���ϸ����������ϸ������������ʾ��Ľ�����йأ�
���ϸ� | �ϸ� | |
���� | 14 | 16 |
�� | 10 | 20 |
��1���Ƿ���90%���ϵİ�����Ϊ���Ա��������ʾ��Ľ�����йأ�
��2���ڳɼ��ϸ��ѧ���У������Ա���зֲ��������ѡȡ9�˽�����̸���ٴ���9���������ȡ5�˷��ͽ�Ʒ�����õ���Ʒ����������ΪX����X�ķֲ��м���ѧ����![]() ��
��
����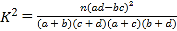
| 0��100 | 0��050 | 0��010 | 0��001 |
| 2��703 | 3��841 | 6��635 | 10��828 |
���𰸡���1��û��90%�İ�����Ϊ���Ա��������ʾ��Ľ�����йأ���2���ֲ��м�������![]()
��������
��1�����ݶ����Լ����˼�뼴���ж�.
��2�������⣬�ɼ��ϸ��������ȡ4�ˣ��ɼ��ϸ��Ů����ȡ5�ˣ�X�Ŀ���ȡֵΪ![]() ���������������ĸ��ʣ��г��ֲ��м����������.
���������������ĸ��ʣ��г��ֲ��м����������.
��1������������������ʾ��
���ϸ� | �ϸ� | �ϼ� | |
���� | 14 | 16 | 30 |
�� | 10 | 20 | 30 |
�ϼ� | 24 | 36 | 60 |
![]() ��
��
��û��90%�İ�����Ϊ���Ա��������ʾ��Ľ�����йأ�
��2�������⣬�ɼ��ϸ��������ȡ4�ˣ��ɼ��ϸ��Ů����ȡ5�ˣ���X�Ŀ���ȡֵΪ![]() ��
��
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ��
��
��X�ķֲ���Ϊ��
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
����![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������C��![]() ���������߽���F��ֱ�߽�������C��A��B���㣬P����������һ�㣬����
���������߽���F��ֱ�߽�������C��A��B���㣬P����������һ�㣬����![]() ��
��![]() �ֱ��������ڵ�C��D����
�ֱ��������ڵ�C��D����![]() ����
����![]() ��
��![]() ���е�ֱ�ΪM��N.
���е�ֱ�ΪM��N.
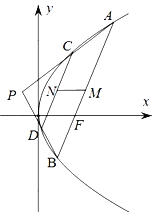
��1����֤��![]() �
�
��2����![]() ����
����![]() �������Сֵ.
�������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����
����![]() ����������Ϊ
����������Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����֪Բ����Ϊ![]() ����Բ������һ����Բ�����ߣ���������Բ
����Բ������һ����Բ�����ߣ���������Բ![]() ����
����![]() ��
��![]() ���㣬
���㣬![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��ͼ����֪![]() ����
����![]() ��ֱ����������Ƥ��
��ֱ����������Ƥ��![]() �ף�
�ף�![]() �ֱ��DZ�
�ֱ��DZ�![]() �ϲ���˵��غϵĶ��㣬��
�ϲ���˵��غϵĶ��㣬��![]() .�ֽ�
.�ֽ�![]() ��Ƥ��
��Ƥ��![]() ������
������![]() ��λ�ã�ʹ��ƽ��
��λ�ã�ʹ��ƽ��![]() ƽ��
ƽ��![]() ������
������![]() ����ͼ��ʾ.��Ҫ����һ������
����ͼ��ʾ.��Ҫ����һ������![]() �ķ������������
�ķ������������![]() ��Ƥ��ֱ������
��Ƥ��ֱ������![]() ��Ƥ�ֱ���������������һ������͵��棬����������������ͬ���ϵ���Ƥ�캸���ܷ���ɣ��������������в��˷Ѳ��ϣ�����Ƥ��Ⱥ��Բ��ƣ���
��Ƥ�ֱ���������������һ������͵��棬����������������ͬ���ϵ���Ƥ�캸���ܷ���ɣ��������������в��˷Ѳ��ϣ�����Ƥ��Ⱥ��Բ��ƣ���
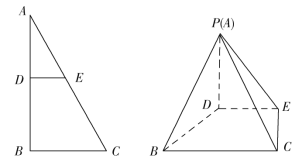
��1����![]() Ϊ
Ϊ![]() �ߵ��е㣬���������������������Ƥ����Ƕ���ƽ���ף�
�ߵ��е㣬���������������������Ƥ����Ƕ���ƽ���ף�
��2������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ������
������![]() �ϵ����ֵ��
�ϵ����ֵ��
��2��������![]() ����3��ֱ��������
����3��ֱ��������![]() ���У���
���У���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ǰn���Ϊ
��ǰn���Ϊ![]() ,��֪
,��֪![]() ,
,![]() ,
,![]() .
.
(1)֤��:![]() Ϊ�ȱ�����,���
Ϊ�ȱ�����,���![]() ��ͨ�ʽ;
��ͨ�ʽ;
(2)��![]() ,��
,��![]() ��ǰn���
��ǰn���![]() ,���ж��Ƿ����������nʹ��
,���ж��Ƿ����������nʹ��![]() ����?�������������nֵ;��������˵������.
����?�������������nֵ;��������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x����g��x���ֱ��Ƕ�����R�ϵ��溯����ż������f����x����g'��x��Ϊ�䵼��������x��0ʱ��f����x��![]() g��x��+f��x��
g��x��+f��x��![]() g'��x����0��g����3����0����ʹ�ò���ʽf��x��
g'��x����0��g����3����0����ʹ�ò���ʽf��x��![]() g��x����0������x��ȡֵ��Χ�ǣ� ��
g��x����0������x��ȡֵ��Χ�ǣ� ��
A.������,��3��B.����3,0��C.��0,3��D.��3,+����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼһ����ֱ������![]() �У�
�У�![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �����ȷֵ㣬
�����ȷֵ㣬![]() ,
, ![]() ��
��![]() ��
��![]() ��������
��������![]() �۵�ʹ�õ�
�۵�ʹ�õ�![]() ��
��![]() �غϣ���ͼ����ʾ������
�غϣ���ͼ����ʾ������![]() .
.
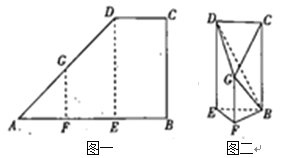
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�����һ���Լ![]() �Ľӽ������εĻĵأ��ط��������ڴ˽�һ���ۺ������й㳡������Ҫ������ͼ��ʾ��һ�����γ��أ����������Ϊ3000ƽ���ף�������Ӱ����Ϊͨ����ͨ������Ϊ2�ף��м�������������������ܽ�������Ϊ�˶����أ���������С������״��ͬ�����ܽ��˶�����ռ�����Ϊ
�Ľӽ������εĻĵأ��ط��������ڴ˽�һ���ۺ������й㳡������Ҫ������ͼ��ʾ��һ�����γ��أ����������Ϊ3000ƽ���ף�������Ӱ����Ϊͨ����ͨ������Ϊ2�ף��м�������������������ܽ�������Ϊ�˶����أ���������С������״��ͬ�����ܽ��˶�����ռ�����Ϊ![]() ƽ���ף�
ƽ���ף�
��1���ֱ���![]() ��ʾ
��ʾ![]() ��
��![]() �ĺ�����ϵʽ��������������
�ĺ�����ϵʽ��������������
��2�����������ʹ![]() ȡ�����ֵ����������ֵ��
ȡ�����ֵ����������ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com