
【题目】已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8.
(Ⅰ) 求动圆圆心的轨迹C的方程;
(Ⅱ) 已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P, Q, 若x轴是![]() 的角平分线, 证明直线l过定点.
的角平分线, 证明直线l过定点.
【答案】(Ⅰ)![]() (
(![]() ) (Ⅱ)见解析
) (Ⅱ)见解析
【解析】(Ⅰ)设动圆圆心C的坐标为( x , y )则![]() 所以,所求动圆圆心的轨迹C的方程为
所以,所求动圆圆心的轨迹C的方程为![]() (
(![]() )
)
(Ⅱ)证明:
设直线l方程为![]() ,联立
,联立![]() 得
得![]() (其中
(其中![]() )
)
设![]() ,若x轴是
,若x轴是![]() 的角平分线,则
的角平分线,则
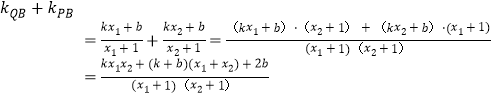
![]() ,即
,即![]() 故直线l方程为
故直线l方程为![]() ,直线l过定点.(1,0)
,直线l过定点.(1,0)
本题考查轨迹方程求法、直线方程、圆方程、直线与圆的位置关系及直线过定点问题.第一问曲线轨迹方程的求解问题是高考的热点题型之一,准确去除不满足条件的![]() 点是关键.第二问对角平分线的性质运用是关键,对求定值问题的解决要控制好运算量,同时注意好判别式
点是关键.第二问对角平分线的性质运用是关键,对求定值问题的解决要控制好运算量,同时注意好判别式![]() 的条件,以防多出结果.圆锥曲线问题经常与向量、三角函数结合,在训练中要注意.本题无论是求圆心的轨迹方程,还是求证直线过定点,计算量都不太大,对思维的要求挺高;设计问题背景,彰显应用魅力.
的条件,以防多出结果.圆锥曲线问题经常与向量、三角函数结合,在训练中要注意.本题无论是求圆心的轨迹方程,还是求证直线过定点,计算量都不太大,对思维的要求挺高;设计问题背景,彰显应用魅力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右顶点与右焦点的距离为
右顶点与右焦点的距离为![]() ,短轴长为
,短轴长为![]()
(I)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为![]() 求直线AB的方程。
求直线AB的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·云南玉溪一中月考)已知函数![]() ,函数g(x)=f(x)-x+1的零点按从小到大的顺序排列成一个数列,该数列的前n项的和为Sn,则S10等于( )
,函数g(x)=f(x)-x+1的零点按从小到大的顺序排列成一个数列,该数列的前n项的和为Sn,则S10等于( )
A. 45 B. 55
C. 210-1 D. 29-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
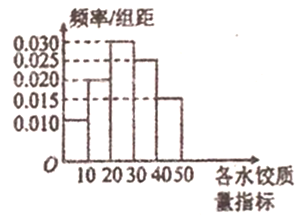
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com