
| A. | [$\frac{9}{8}$,2] | B. | [$\frac{3}{4}$,+∞) | C. | [$\frac{3}{4}$,2] | D. | (0,$\frac{3}{4}$] |
分析 求$\overrightarrow b$,$\overrightarrow a$的夹角的范围,代入投影公式计算最值.
解答 解:∵|${\overrightarrow a$-2$\overrightarrow b}$|≤4,
∴|${\overrightarrow a$|2-4${\overrightarrow a$•$\overrightarrow b}$+4|$\overrightarrow b}$|2≤16,
∴9-4${\overrightarrow a$•$\overrightarrow b}$+16≤16,
∴${\overrightarrow a$•$\overrightarrow b}$≥$\frac{9}{4}$,
设$\overrightarrow b$,$\overrightarrow a$的夹角为θ,
则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$≥$\frac{3}{8}$,
又∵cosθ≤1,
∴$\frac{3}{8}$≤cosθ≤1,
∴$\frac{3}{4}$≤|$\overrightarrow{b}$|cosθ≤2,
故选:C
点评 本题考查了平面向量数量积的运算与应用,求出向量夹角是关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | sin(α+β)=sinαcosβ+cosαsinβ | B. | sin(α-β)=cosβsinα-sinβcosα | ||
| C. | cos(α-β)=cosαcosβ-sinαsinβ | D. | cos(α+β)=cosαcosβ-sinαsinβ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 评分等级 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
| 小学 | 2 | 7 | 9 | 20 | 12 |
| 中学 | 3 | 9 | 18 | 12 | 8 |
| 学校类型 | 满意 | 不满意 | 总计 |
| 小学 | 50 | ||
| 中学 | 50 | ||
| 总计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{1}{10}$ | p |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
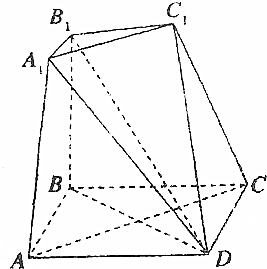 如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.
如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线的一支,这支过点(1,$\frac{1}{2}$) | B. | 抛物线的一部分,这部分过点(1,$\frac{1}{2}$) | ||
| C. | 双曲线的一支,这支过点(-1,$\frac{1}{2}$) | D. | 抛物线的一部分,这部分过点(-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com